What is Group Charting for Multi-stream Processes
Multi-spindle screw machines, multi-cavity injection molds, multi-head filling machines, and other multi-stream processes pose significant problems for traditional pencil and paper SPC systems. These problems are largely driven by the need to economize and speed production, therefore limiting periodic measurements to one piece per stream. Let’s examine a hypothetical application for a twelve cavity injection mold using pencil and paper SPC charting.
How this Application is Typically Used
In this application, a paper x-bar & R chart with a subgroup size of 12 (one per stream) is typically used. In theory, movement on the x-bar chart indicates common mode problems (those that affect all cavities, spindles, etc.), and movement on the Range chart indicates problems with individual cavities. However, although the cavities are identical in theory, in practice there are fixed differences. While these inherent differences are built into virtually every multi-stream process, their magnitude varies from machine to machine.
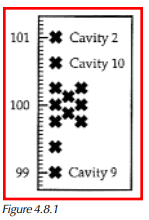
In this example, we will assume that the nominal part size is 100 and that the ±3σ of each individual cavity is ±0.5, while the highest mean for any one cavity (Cavity 2) is 101, and the lowest mean for any one cavity (Cavity 9) is 99 (see Figure 4.8.1).
For the x-bar chart, the actual problems become apparent when we examine the x-bar control limit calculations. While more sophisticated methods are available, many users rely on the simple use of A2 tables. Using an A2 table and an R-bar of 2.0 (due primarily to the inherent difference between Cavity 2 and Cavity 9) we come up with control limits of 100.54 and 99.46. These control limits are about four times wider than would ordinarily be calculated for a subgroup size of 12 and a ±3σ value of ±0.5 for individuals. These wider than normal control limits mean that either only huge errors will cause x-bar control limit violations or control limits based on other than R-bar must be used.
Sensitivity of the Method
As bad as things are on the x-bar chart, things are worse on the Range chart. In the example above, an R-bar of 2.0 is used to calculate an Rucl of 3.44. Assume that Cavity 2 develops a small but growing blockage that causes each subsequent sample to be reduced by 0.5. Given the distribution of the rest of the cavities, the range chart would not go out of control until Cavity 2 had marched down eight steps of 0.5 to a value of 97. The insensitivity of this method is demonstrated by the fact that a value of 97 for this cavity represents a whopping -24 σ with an assumed 6 σ spread of 1.0.
These fixed differences in cavities cause additional problems when one or more streams are taken off line. Assume that Cavities 2 and 10 have been plugged. This would cause a downward shift on the x-bar chart of almost 1.0. Adjustments made to the machine to “correct” for this shift will increase, rather than decrease, variability in the final product.
The Range chart is subject to similar difficulties. Assume that Cavities 2 and 9 have been plugged. In this case, there would be a decrease in subgroup ranges of almost 1.0. This may seem to be a good thing at first. However, on closer inspection, we find the R chart’s ability to indicate a problem associated with a single stream is degraded by the fact that a given stream must demonstrate even greater error to generate a control limit violation.
Intrastream and Interstream
Finally, when intrastream variability (within a single stream) is dominant and fixed, and interstream differences (between cavities, spindles, etc.) are negligible, bringing streams off line will have different adverse effects. For example, assume the mean and range of four pieces is plotted on a control chart with the control limits calculated for six pieces. In this case, the x-bar chart is much more likely to generate false out of control conditions as is substantially wider than. Conversely, the range chart will be more likely to hide out of control conditions.
To sum up, using one large subgroup and paper SPC charting for multi-stream processes causes the following problems:
- Traditional control limit calculation methods yield insensitive limits.
- Inherent differences mask actual variability.
- Trends and shifts on individual streams are ignored.
- The relationship among the streams is hidden.
- Bringing individual streams in or out of service can create misleading indications on the control chart.
These problems could largely be addressed by maintaining control charts for each individual stream, ideally using X & mR for cavities with Cpk ≥ 3.0 and x-bar & R for cavities with Cpk < 3.0. Unfortunately, complexity and time constraints preclude this preferred methodology for most applications.
How can we avoid these problems?
Given the constraint of single piece per stream sampling, an ideal system would provide the following:
- One chart that summarizes the status of the process for quick analysis.
- X & mR (moving range) charts for each stream are available for troubleshooting.
- Run and shift trend analysis for individual streams, and for the combined output.
- A means to easily identify consistently high or low streams.
- The ability to analyze variability independent of fixed differences.
- High-speed data entry.
- The ability to quickly identify significant changes within a single stream.
- The ability to deal with streams being brought on and off line.
- The ability to detect a change in the relationship among streams.
Electronic Data Collection Provides a Solution
In no way can pencil and paper charting economically satisfy all these requirements. A multi-stream application demands electronic data collection and analysis to reduce the time required to both collect the data and to “double” analyze common mode and individual stream problems. The answer is modern SPC electronic data collectors with group charting. These data collectors can provide all of the required analysis accurately, while also reducing data collection time.
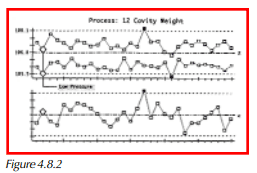
The group chart is perhaps the most widely accepted tool for multi-stream applications (see Figure 4.8.2). The group chart plots the highest and lowest and lowest piece value (or mean of the sample if more that one piece per stream is sampled) on the X chart, and the largest moving range (or range for the entire sample if more that one piece per stream is sampled) on the R chart. When some streams are sampled as individuals and others as means, the X (x-bar) control limits on the group chart should normalize the plotted points to the control limits (3σ or 3, respectively), as the range limits should with the points on the R chart.
Conceptually, as long as the high X point is below upper action limit, and the low X point is above lower action limit, the process is running acceptably. And since the range chart shows the maximum range from any one stream to its own previous value, the range chart is very sensitive to changes by any stream, regardless of fixed interstream differences. Users unaccustomed to group charts should be aware that the average plotted mR on the group chart will be higher than on an X & mR chart, as only the maximum mR among all streams is plotted. A group chart may be scaled by the actual measured values, or if desired, control limits may be calculated for each individual stream and a chart normalized to control limits may be used. The latter option may be most useful in applications with substantial fixed interstream differences that may not be eliminated.
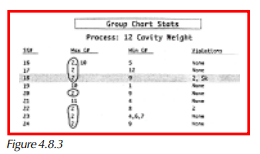
While the group chart is the most convenient method for day-to-day monitoring, a tabular report is more useful for identifying consistently high or low streams. The group chart statistics report shown in Figure 4.8.3 clearly shows the tendency of Cavity 2 to run higher than the rest of the cavities.
How Does The Operator Be Prompted by the Data Collector
Using our 12-cavity example, the operator would be prompted by the data collector to measure one piece from each cavity in sequence, after which the group chart would be displayed. If one or more of the cavities had to be plugged for some reason, the prompts for those cavities could be turned off. The ability to customize the prompting sequence in real-time is a critical convenience for multi-stream process monitoring.
In the background, much more could be accomplished. Each of the active cavities could be monitored for trends and/or control limit violations individually. The change in each cavity from its own previous sample would be checked for unexpectedly large changes. The overall average and range could be monitored, and, unlike pencil and paper charting, the plots could be automatically adjusted to accommodate various sample sizes as cavities were plugged in or brought back online. In addition, depending on the process, error corrections could be fed back directly or indirectly to the machine.
The group chart is just one of the many convenient and powerful tools available in a modern quality data collection and analysis system for multi-stream applications. Without going into that entire array of tools, perhaps the most important supporting tool to the group chart is the electronic data collector’s ability to show the relationship among cavities on the same data used for group charting. Figure 4.8.4 shows the data for one subgroup plotted to show each cavity. Since the even numbered cavities are all on the right side of the die, the chart is a clear indication of a source of assignable variability.
Cost-prohibitive for Manual Methods
In summary, modern electronic data collection and analysis offers multi-stream processes — such as multi-spindle screw machines, multi-cavity injection molds, and multi-head filling machines — the economy of decreased data collection time at increased reliability, and tailored charting and effective analysis techniques that are cost-prohibitive for manual methods.