How to Estimate Scrap and Rework
One of the most valuable applications of statistical quality control is that of reducing scrap and rework. The reduction of scrap and rework alone can pay for the installation of an SPC system in a very short period of time. This section covers calculating the amount and cost of scrap and rework, and possible methods for reducing scrap and rework.
Estimating by Calculating the Area
Estimating scrap and rework can be done by analyzing the data that was collected in the capability study. It is done by calculating the area under the normal curve that falls outside the specification limits. This is most reliable if the distribution of the measurements is reasonably normal. An area under the normal curve z-table (Table A-3 in the Appendix) is needed for this calculation. Z-tables were introduced in Chapter 2. Let’s review how to use z-tables to find the area outside the specification limits (USL and LSL stand for upper specification limits and lower specification limits, respectively):
1) Calculate (LSL – Mean) ÷ Sigma.
2) Look up the calculated value from areas of normal curve table (Table A-3).
3) Calculate (USL – Mean) ÷ Sigma.
4) Look up calculated value from areas of normal curve table (Appendix, Table A-4).
5) The value calculated in Step 4 gives the area from the left tail to the USL. Subtract this value from 1 to get the area above the USL.
6) Add the values from Steps 2 and 5 to obtain the total area outside the specification limits.
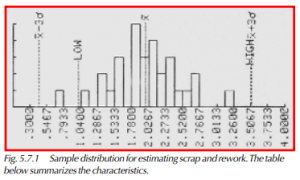
As an example, let’s use the data from Table 5.7.1. Calculations are:
1) (LSL – Mean) ÷ Sigma = (1.0 – 2.0) ÷ 0.5 = – 2.0.
2) Table value = 0.0228.
3) (USL – Mean) ÷ Sigma = (5.0 – 2.0) ÷ 0.5 = 6.0.
4) Table value = 1.0.
5) 1 – 1.0 = 0 (no area outside the USL).
6) 0.0228 + 0 = 0.0228.
Cost of Scrap and Rework
Total scrap/rework is thus about 2.28%. In addition to calculating the amount of scrap and rework, you can also arrive at a cost. To estimate the cost of scrap and rework we first must estimate the costs of scrap per part and rework per part. If rework costs more than scrap (this condition should be rare) it is more cost-efficient to scrap those parts that require rework.
The cost of scrap and rework is equal to:
Rework cost = Scrap cost = (5.7.1)
(Rework cost/part) (Scrap cost/part)
(% rework) (% scrap)
(number of parts) (number of parts)
As an example, let’s examine the conditions shown in Figure 5.7.1 and Table 5.7.2. Samples below LSL are scrapped, while samples above USL are reworked.
First we must calculate the amount of material above USL and below LSL. This is similar to our example above:
1) (LSL – Mean) ÷ sigma = – 2.0.
2) Table value is 0.0228.
3) (USL – Mean) ÷ sigma = 3.0.
4) Table value is 0.9987, so area above USL is 1 – 0.9987 = 0.0013.
Next we calculate the cost:
Cost of scrap = $5.00/part × 0.0228 = $0.114/part
Cost of rework = $2.00/part × 0.0013 = $0.0026/part
Total cost = $0.114 + $0.0026 = $0.1166/part
Estimation Using Non-Normal Data
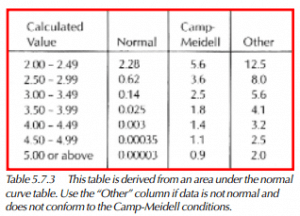
Estimates for scrap and rework on non-normal data are less reliable than similar calculations on normal data. This section will separate data into three categories: data that is roughly normal, data that conforms to the Camp-Meidell conditions, and other data. Under CampMeidell conditions the mode is equal to mean (mode is in the tallest bar of a histogram), and frequency declines continuously on both sides of the mode (Table 5.7.3). Use the following procedure for this:
1) Calculate (Mean – LSL) ÷ Sigma.
2) Look up the calculated value in Table 5.7.3.
3) Calculate (USL – Mean) ÷ Sigma.
4) Look up the calculated value in Table 5.7.3.
5) Sum of the two values in Step 4 is the estimated amount of scrap or rework.
As an example, let’s examine the condition shown in Figure 5.7.2 and Table 5.7.4. The data does not meet the Camp-Meidell conditions; therefore, the “Other” column is used on the chart.
1) Index for area under normal curve table (Table A-2) is: (2.0 – 1.0) ÷ 0.5 = 2.0.
2) Area below LSL is 12.5% (from Table 5.7.3).
3) Index for area under normal curve table is: (5.0 – 2.0) ÷ 0.5 = 6.0.
4) Area above USL is 2.0% (from Table 5.7.3).
5) Total scrap and rework is: 12.5% + 2.0% = 14.5%.
Best Method for Reducing Scrap and Rework
The best method for reducing scrap and rework is to improve the manufacturing process and make better parts. This option is not always available, due to limitations in materials or equipment. A second option for reducing the cost of scrap and rework involves shifting the mean of a process. We conclude with an example of how shifting a process mean can minimize scrap and rework costs. Rework costs $0.20 per part and scrap costs $2.00 per part.
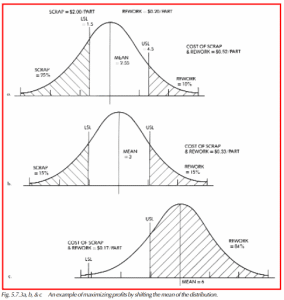
Figure 5.7.3a shows a process where scrap accounts for 25% of production, and rework accounts for 10% of production. The cost of scrap and rework is $0.52 per part.
After shifting the process to the midpoint of the tolerance, scrap accounts for 15% of production and rework accounts for 15% of production (Figure 5.7.3b). The cost of scrap and rework is $0.33 per part.
When the process is shifted to the extreme of having no scrap, rework accounts for 84% of production (Figure 5.7.3c). The cost of scrap and rework is $0.17 per part. Although the cost of scrap and rework has been reduced significantly, the cost of quality (which includes the labor of checking parts) may actually be more than in the other examples.
The distribution is assumed to remain stable when the mean of the process is shifted. By using statistical methods to monitor the expected amount of scrap and rework, it is possible to reduce costs through fairly simple means (e.g., machine adjustments).