How to Minimize total cost of Inspection and Repair
An entirely different perspective on incoming lot inspection is obtained if one views the goal to be minimizing the total cost of incoming parts inspection, plus minimizing the costs of repairing and testing assemblies that fail because of defective parts being incorporated into these assemblies. Dr. W.E. Deming offers some simple mathematical proofs to show that the least-cost method of production is either no incoming inspection or 100% inspection (W.E. Deming, 1982, Chapter 13).
To illustrate this point, some suppositions must be made:
- Initially, a single incoming part will be considered. (The method can be extended readily to multiple parts.)
- Every assembly produced is functionally tested.
- If the incoming part is defective and goes into an assembly, the assembly will fail its test. (If the part is not defective, by definition, the assembly will pass its test.)
To examine this premise mathematically, we need a few definitions:
p — The average fraction defective in the incoming part receipts (say for one day).
k1 — The cost to inspect one incoming part.
k2 — The cost to fix and retest an assembly that had a defective part.
k1/k2 — The breakeven percentage point.
Several conclusions can be drawn from this analysis:
- Treating a clear case 1 situation as a case 2 situation (test every part) will maximize the overall cost, as will the inverse.
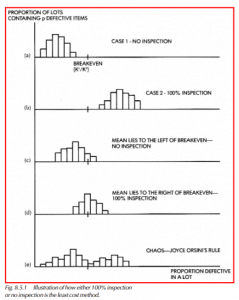
- In cases where defective parts are binomially distributed around a mean (p), the same case rules apply even though the distribution of defective parts straddles the breakeven point (Figure 8.5.1, parts c and d).
- One must be sure, for a case 1 decision, that p will be less than breakeven. This requires that the purchaser or the vendor keep the production process for the incoming part under statistical control — at a minimum, test small samples from every lot.
- If there is no clean grouping, the process is said to be in chaos (Figure 8.5.1, part e). In this case, and assuming that the breakeven point is greater than 0.002, Joyce Orsini’s rule may be used (see the references at the end of the chapter): take a random sample of 200 parts from a lot. If there is no defective part in the sample, accept the remainder as is. If one or more defective parts are found, replace them and inspect the rest of the lot.
- In the event of work being done to a semi-finished part, analysis shows that the same case 1 and case 2 rules apply where k2 is now the average loss from downgrading or scrapping finished product that fails.
Comparing the Deming method with standard acceptance plans, such as the Dodge-Romig tables and MIL-STD-105E, leads to some surprising conclusions. For example, the theory behind the Dodge-Romig tables is said to minimize the cost of inspection to achieve a prescribed level of quality or percentage of acceptable parts, rather than minimizing the total cost.
Anscombe says, “It is time to realize what the problem really is, and solve that problem as well as we can instead of inventing a substitute problem that can be solved exactly but is irrelevant,” (Journal of the American Statistical Association, 1958, pp. 702-719).
It is argued that, in many circumstances, prescribing an acceptance plan will cost considerably more in total than 100% inspection. It is argued further that if the process producing the parts were in good statistical control, tests of samples would provide no useful information. Therefore, the ideal situation is for the vendor to supply proof that the production process is in statistical control.