Introduction to Control Charts
The problem identification and analysis tools described in the last article provide a means to prioritize and analyze individual problems. The result of this analysis will suggest specific problems or processes that require further work using the next step in our SPC model: Use SPC to bring the key variables into control. These selected variables or processes may include items such as:
- Outer diameter of a bushing
- Fill weight of a soda bottle
- Torque of a headbolt on an engine
- Hardness of a transmission gear
- Solder defects on a printed circuit board
Common and Assignable Cause Variation in Control Charts
In each of these cases, the next objective is to reduce the variation in the characteristic in question, without making significant changes to the production process. The discussion about variation in Chapter 1 identified two causes for variation — common causes and assignable causes. Common cause variation is inherent to any process that shows stability over time. Assignable cause variation results from significant and identifiable changes in the process, such as a new lot of raw material entering the process, a new operator at the process, or a change in tooling. It is easy to see that reducing variation through eliminating assignable causes is more practical than reducing variation through eliminating common causes. Process control charts are the best tool available for identifying and eliminating assignable cause variation.
What are Control Charts
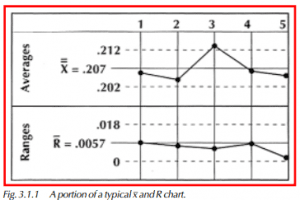
Control charts provide a graphic comparison of a measured characteristic against computed control limits. They plot variation over time and help us distinguish between the two causes of variation through the use of control limits. These limits are vital guidelines for determining when action should be taken in a process. Figure 3.1.1 shows a portion of a typical x & R chart. It is important to note the following elements:
1) Each of the points on the x portion of the chart represents an average of one subgroup’s readings. Because each point is an average value, all of the points taken together will tend to be normally distributed if they are from a process showing stability (refer to the Central Limit Theorem in Section 1.3).
2) The dashed-line control limits are drawn at approximately +3 and –3 standard deviations from the central line on the x portion of the chart. Because points on the chart from a process showing stability tend to be normally distributed, we now expect 99.73% of all the points to fall between the two control limits (refer to the discussion on standard deviation in Section 1.3).
3) Point #3 on Figure 3.1.1 is beyond the upper control limit for x. There are four possible explanations for this occurrence: a measuring error, a plotting error, an assignable cause, or the possible exception to the probability that 99.73% of all common causes will fall within control limits.
4) Each x value on the chart represents an average of individual readings in the subgroup; therefore, we must also examine the range chart to determine the variability of the individual readings in that subgroup.
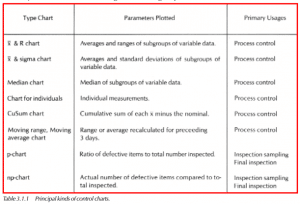
Principal Kinds of Control Charts
There are essentially two kinds of control charts — control charts for variables data (quantitative data or measurements), and control charts for attribute data (qualitative data or counts). See Table 3.1.1. Variables control charts are more sensitive to changes in measured values, and, therefore, are better for process control. Control charts for attribute data are useful for other reasons; data is easily obtained, and often does not require a specialized means of data collection, and attribute data charts are the least costly to use.
x & R Chart
The x & R chart is the most common form of a control chart for variables data, and one of the most powerful for tracking and identifying causes of variation. The xchart is a continuous plot of subgroup averages. The R chart is a continuous plot of subgroup ranges. A subgroup typically ranges in size from 2 to 20 samples. When using subgroup sizes greater than 10 samples, it is recommended that you use a sigma control chart rather than range.
x & s Chart
Known as x and sigma chart, the parts of this chart, like the x & R chart, are always used as a pair. The sigma chart is a somewhat more accurate indicator of process variability than an R chart, especially with a larger-sized subgroup. However, using the sigma chart, it is more difficult to calculate sigma and users often have a more difficult time understanding and interpreting the sigma values.
Median Chart
This chart combines both the x & R information into one graph. The median is the middle value when data is arranged according to size. A median chart yields similar conclusions to the x & R chart, and is easy to use. Typically, median charts are used with subgroup sample sizes of 10 or less.
Control Chart for Individuals
A control chart for individual samples is used when process control must be based on individual readings rather than subgroups: i.e., such as when measurements are expensive or destructive, or the result of a single daily lab test. Control limits for a chart of individuals should be based on the moving range. Chapter 4 describes control charts for individuals in greater detail.
Cumulative Sum (CuSum) Chart
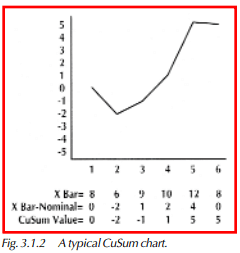
A CuSum chart looks at subgroup averages in a different way than the x & R chart. On a CuSum chart, each point represents the cumulative sum of each x value minus the nominal value. Figure 3.1.2 shows a CuSum chart. In this example, the nominal value is 8. The first x value is also 8. Since 8 – 8 = 0, the first CuSum value is 0. The second x value is 6. To determine the second CuSum value, the nominal value (8) is subtracted from the x value (6) and added to the previous CuSum value (0): 6 – 8 = -2; -2 + 0 = -2. The third x value is 9. The third point on the chart is determined by: 9 – 8 = 1; 1 + -2 = -1.
Basically, the CuSum chart exaggerates the shift from nominal. If successive x-bars fall on both sides of the nominal, the chart remains fairly flat. But if two or more successive x-bars fall on the same side of the nominal, the curve begins to rise and fall quite rapidly. The chart, therefore, is much more sensitive to a sustained shift away from the nominal.
Moving Average Moving Range Chart
This chart is used primarily in industries where the output of a process is very stable from piece to piece, but may vary from day to day or week to week: e.g., a metal stamping application where the dies wear slowly, or a plating application where the same chemical bath is used each day. In this example, a three-day moving average chart would plot a point for Friday by averaging Friday’s reading with readings from Thursday and Wednesday. Similarly, a moving range chart would plot the range over a three-day period each day. These charts tend to dampen what would be a single out-of-control reading on the x & R chart, and distribute effects over a longer period of time. Moving average and moving range charts are described in greater detail in Chapter 4.
p-Chart
The p-chart (percent defective chart) is an attribute chart for the percentage of defective items in a subgroup, when the subgroup is not necessarily of a constant size from inspection to inspection. Fraction defective is the ratio of defective items to the total number of items inspected, which is another way of expressing the percentage.
np-Chart
The concept of the np-chart is the same as the p-chart, except that the np-chart represents the actual number of defective items in the subgroup, rather than the fraction. The np-chart requires a constant subgroup size. It would be better to use the np-chart if the actual number of defectives is more meaningful or simpler to report than the proportion value presented by the p-chart.
c-Chart
The c-chart is a special type of attribute control chart that uses the number of defects instead of the number of defectives. In cases where a unit can contain many defects, the c-chart is a practical alternative. Each point on the chart represents the number of defects in the subgroup. The c-chart should be used only when the sample size making up the subgroup remains constant from inspection to inspection. The c-chart is particularly useful where a unit is likely to contain many defects.
u-Chart
The u-chart is similar to the c-chart in that it tracks individual defects. Unlike the np-chart, the u-chart may use subgroups of varying sizes. A single point on a u-chart represents the average number of defects on each part in a subgroup. For example, if the subgroup size equals 10, and there are 5 defects in that subgroup, the u value would be 0.5. This signifies an average of 0.5 defects on each part in that subgroup.