Introduction to Non-Normal Distributions
This section concerns itself with distributions of a continuous nature, as opposed to discrete. Continuous implies that the occurrence of values within a range or interval is random, and not of a countable, finite set. Examples of discrete distributions include binomial and poisson. The most familiar continuous distribution is the normal (or gaussian) distribution.
The Moments in Dealing with Frequency Distribution
Frequently in statistics, one is able to compute several moments of a distribution. The first four moments are related to mean, variance, skewness, and kurtosis, respectively. In dealing with frequency distributions, these four moments indicate location, spread, symmetry, and peakedness.
For the normal (gaussian) distribution, the skewness (or symmetry) is equal to zero (0), while kurtosis is equal to three (3). The skewness value of 0 indicates a symmetrical distribution. The kurtosis value of 3 is a relative measure. In general, to “normalize” the kurtosis statistic, 3 is subtracted from the statistic before reporting.
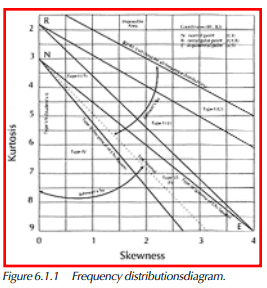
There are a variety of other distributions that necessarily have different skewness and kurtosis characteristics. Figure 6.1.1 shows where some of those distributions fall in relation to skewness (β1) and kurtosis (β2). Within the figure, several distributions are depicted:
– Normal – Beta
– Exponential – Gamma
– Rectangular – Student’s t
– Log-Normal – Chi-Square
As can be seen, the normal distribution occurs only at a point within the entire graph (β1=0, β2=3). It is common to assume that data is normally distributed, unless proven to be otherwise. When the skewness or kurtosis differ significantly from the values associated with the normal distribution, there are several techniques used to describe the frequency distribution (or bell-curve).
These techniques involve either
1) Assuming that the data may be described definitely by one of several other well-known distributions (Exponential, Log-Normal).
2) Transforming the data (Johnson Transformation).
or
3) Using curve-fitting techniques (Pearson System, Weibull Distribution).
Each of the above shall be described and demonstrated.