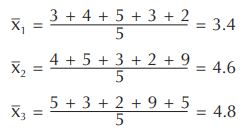What is the Moving Average Control Chart
It is often true that making subgroups from a process is impractical. In some situations, the time required to measure a single observation is so great that repeat observations cannot be considered. These are occasions when moving averages and moving ranges are more in accord with manufacturing practice than ordinary averages and ranges. The method of moving averages and ranges is particularly suitable for lines of production that require some time to produce a single part.
What to Consider about Moving Average
To understand what is meant by a moving average, consider these ten parts and their measurements: 3, 4, 5, 3, 2, 9, 5, 2, 6, and 8. We can break up these ten parts into two subgroups of five each, and calculate the average of the first group and the average of the second group. These would be ordinary averages. If we applied moving averages, however, we would average the first five, then drop the first sample measurement; add the sixth, and average the new set of five; then drop the second sample measurement, add the seventh, and average this new set of five, and so on. Numerically, for the first three x values calculated with this method, we would have:
The above are moving averages of five samples. Moving ranges of the five samples are the ranges of these same subgroups. Here are the range calculations and values:
R1 is the range of 3, 4, 5, 3, 2 = 3
R2 is the range of 4, 5, 3, 2, 9 = 7
R3 is the range of 5, 3, 2, 9, 5 = 7
By adding to our previous sample measurements each new sample measurement (as the part is produced and the oldest sample is dropped), our moving average and moving range gives the usual control and an up-to-date picture of the process.
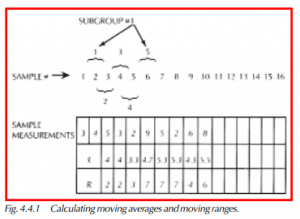
Figure 4.4.1 illustrates one technique for combining sample measurements for moving averages and moving ranges on x̄ & R charts. In this example, you can see we are using a moving group size of three, grouping three measurements together. Subgroup 1 consists of sample measurements 1, 2, and 3. Subgroup 2 consists of sample measurements 2, 3, and 4, and so on.
Steps for Creating a Moving Average, Moving Range Control Chart
1) Select the characteristics to monitor.
2) Select the moving average group size. (We will use three in our example.)
3) Measure your first sample part and record it as Sample 1.
4) Measure your second sample part and record it as Sample 2.
5) Measure your third sample part and record it as Sample 3.
6) Determine the x̄ & R values.
7) Plot these values on the chart as Subgroup 1.
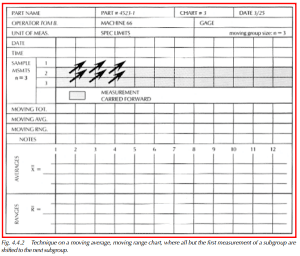
8) Carry forward Samples 2 and 3 to Subgroup 2. Place Sample 2 where Sample 1 was, and Sample 3 where Sample 2 was. (See Figure 4.4.2.) These measurements will be combined with the next sample part measurement to form Subgroup 2.
9) Determine the x̄ & R values.
10) Plot these values on the chart as Subgroup 2.
11) Repeat Steps 8 through 10 until 30 subgroups (minimum) are collected.
12) Calculate x̄ & R values.
13) Calculate control limits using standard x̄ & R formulas for the appropriate sample sizes.
14) Continue monitoring the process.
Important Characteristics of Control Charts
These control charts have some important characteristics. Since we are dealing with moving averages and moving ranges, the plotted points are not independent of each other. Each point reflects the influence of two or more of the same observations. This influence extends over a greater distance when the average involves many observations. Therefore, several points in a row outside or near the control limits do not have the significance that they would on an ordinary chart on which points are independent. Also, temporary fluctuations in the process are likely to be overlooked, since the averaging process tends to decrease the degree of variation. Out-of-control points on the R chart indicate the presence of abnormal short-term variability within the time period during which the data was collected. Therefore, the interpretation of these charts must be somewhat different than the regular Shewhart charts, and they must be more carefully considered.
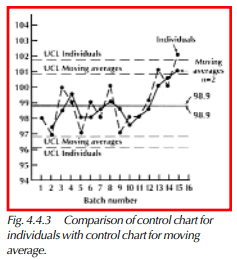
It should be noted that if we compare individuals with moving averages, we see that the use of moving averages reduces the noise of the process, but the major patterns of the charts remain similar. See Figure 4.4.3. The control limit lines are different, as we would expect, since the variability of averages is less than that of individuals, as shown with the Central Limit Theorem (see Chapter 1). The lower degree of variability that moving average charts possess gives them greater power than individuals charts to detect true changes in the process.