What are Nominal Charts
Nominal charts allow more than one part number to be plotted on the same control chart, using the same scale. This reduces the number of charts needed to monitor part numbers and illustrates the effects of the process over time and variation among different part numbers. Because it’s the process and not the parts we’re monitoring, we have to form parts families. As long as they’re made with the same material, method, and machine, parts can be put into a family. The parts within each family can be different sizes, and since the same process makes these parts, they share common traits.
Limitations of Nominals Charts
Although nominal charts can be useful in some manufacturing processes, there are four limitations that should be noted.
1) The variation (standard deviation) of each part number being monitored must be similar. If the variation is not similar, the suspected part number(s) should be plotted on a separate nominal chart.
2) The parts must be produced using the same process — machine, method, and material.
3) The units of measure must be the same.
4) The subgroup size must remain constant.
Coding in Nominal Chart
Before we discuss the steps involved in creating a nominal chart, we have to define coding. In coding numbers, two values must be known: the nominal value and the unit of measure. The nominal value is the desired mean (target) value for the particular dimension. The unit of measure indicates the precision with which the measurements are to be made. This is illustrated in the following example.
Let us suppose we manufacture bearings. The specification for these bearings is 0.500 ± 0.005. The nominal value is the 0.500 value. Let us also suppose that we measure these bearings with a caliper and read to the nearest thousandth of an inch. This, then, would be the unit of measure. Now, instead of recording the entire measurement, we can record coded values. The measurements can be recorded as a certain number of increments above or below the nominal value.
If the nominal value is 0.500 with a unit of measure of 0.001, we code the following measurements using this formula:
Table 4.2.1 shows a listing of the actual and coded values for this example. The +1 indicates a dimension of 0.001 above nominal, and the -1 indicates a dimension of 0.001 below the nominal of 0.500. These coded values are often multiplied by the unit of measure for graphing purposes.
Steps for Creating a Nominal Chart
1) Select the key variable to monitor for each part.
2) Identify the nominal value of the specification.
3) Measure your first sample part.
4) Subtract the f nominal (from Step 2) from the actual value (from Step 3).
5) Divide the result from Step 4 by the unit of measure. These coded values are used in place of actual values to make the numbers easier to calculate.
6) Record the reading as sample measurement #1 on the x & R chart.
7) Continue with Steps 2 through 5 until subgroup #1 is complete.
8) Determine the average (x) and the range (R) for the subgroup.
9) Multiply the results from Step 8 by the unit of measure.
10) Plot the x & R on the control chart.
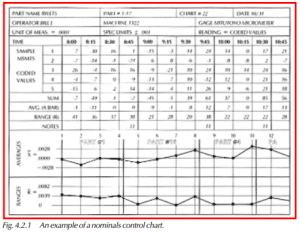
11) Continue with Steps 2 through 7 until this part is done running. Then start all over again with each new part number change. Be sure to document when a new part number starts. On the example control chart shown in Figure 4.2.1, see how new parts were started after subgroups 4, 8, and 11.
12) Continue monitoring the process until 20 subgroups have been collected.
13) Calculate the X & R using the standard formulas.
14) Calculate UCLK and LCLK using the standard formulas. By subtracting each sample measurement from its nominal, we’re actually monitoring the process deviation from that point. This enables us to monitor many different parts sizes from the same process.
Interpretation of Nominal Charts
The interpretation of nominals charts is the same as Shewhart x̄ & R charts. There should be no obvious trends or patterns in the data, beyond what would normally occur by chance. As with x̄ & R charts, the goal is to maintain a constant level of statistical control and to take appropriate action when that level deviates.