What is Scatter Diagram
Once we have identified the elements contributing to our problem, we must determine which causes are truly related to our effect. One tool that can be used to identify a true relationship, or lack of relationship, is the scatter diagram. A scatter diagram is a graphic representation of the relationship between two items. When drawing a scatter diagram, we choose one variable that we believe affects the end result.
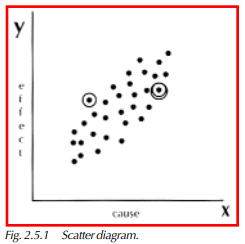
We then change the level of the variable, such as the temperature of a plating bath, and measure the end result, or plating thickness. It is recommended that 50-100 pairs of data be collected. These do not have to be 50-100 different levels of our variable (plating temperature). We can run multiple trials at the same variable level to determine the consistency of the end result. Once we have collected our pairs of data, we can then draw the scatter diagram shown in Figure 2.5.1. The vertical axis of the diagram is the end result (effect) of our test. The horizontal axis is the variable (cause) we were changing (see how this relates to our cause and effect diagram). The lengths of the two axes should be about the same so the diagram is easier to interpret.
Now each of the data pairs can be plotted on the diagram. If two or three points fall at the same place on the diagram, circles can be drawn around the original point to indicate multiple results at this location.
Correlation Table
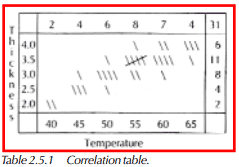
Another method called a correlation table can be used to diagram the data, especially if a large amount of data was collected or many of the same data values are obtained (see Table 2.5.1). The correlation table not only gives a graphic representation of the relationship between the variable and the result, it also lists the frequency of occurrence at each test level. With small amounts of data, the correlation and frequency is easily determined from the scatter diagram. With large amounts of data, this becomes more difficult to interpret.
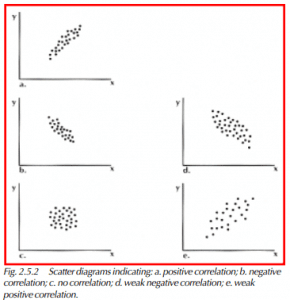
Once the data is plotted, we can analyze the scatter diagram for correlation (relationship) between the cause and the result of the tests. The following diagrams show the types of patterns we may observe (see Figure 2.5.2). Note the following information as you look at the diagrams:
Positive Correlation
A positive correlation is found when an increase in the variable (cause) leads to a corresponding increase in the result (effect). A strong positive correlation means that an increase in the variable leads to a definite corresponding increase in the result. A weak correlation means that an increase in the variable results in some increase in the result, but it is less dramatic and more difficult to identify.
Negative Correlation
A negative correlation is found when an increase in the variable leads to a decrease in the result. Again, a strong negative correlation indicates a definite decrease in the result when the variable increases. A weak correlation indicates a weaker relationship between the variable and the result.
No Correlation
No correlation occurs when there is no real relationship between the variable and the result.
In the example shown in Figure 2.5.1, we see that we have a fairly strong positive correlation. This means that within our testing range, an increase in the plating temperature should result in an increase in the plating thickness. Note: Scatter diagrams are useful for comparing two variables. However, they are not a substitute for regression and can be misused easily.
Correlation Coefficient
Once we have plotted the points on the scatter diagram and we have visually examined it for correlation, we can also calculate a numeric value called a correlation coefficient (r), to describe the correlation between our items. There are different methods of calculating correlation coefficients, but all of the commonly used methods will result in a value between –1 and +1. A value of –1 shows a perfect negative correlation, a +1 shows a perfect positive correlation, and a 0 shows no correlation. Values falling between 0 and +1, or 0 and –1, show a weaker correlation between the items being studied. The significance of the correlation coefficient value depends upon the size of the value and the number of samples used in the calculation.
As the value of the coefficient gets closer to ±1, the strength of the correlation increases. The actual calculation of the correlation coefficient (r) and its significance are given below. For further information — beyond the scope of this book — on correlation coefficients and calculation of standard error, refer to Juran’s Quality Control Handbook and Duncan’s Quality Control and Industrial Statistics.