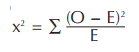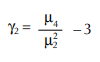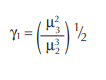What are the Tests for Normality
Abnormal distributions are any distributions other than the normal distributions described in Chapter 1. Figures 5.5.1, 5.5.2, and 5.5.3 show examples of three common, abnormal distributions. Abnormal distributions may or may not be characteristic of the process itself, depending on the size of the sample, the probability of the sample being an accurate reflection of the process, and other factors. A process can be in control and still have a abnormal distribution. An example would be a part that is machined with stops that prohibit making it too small. The distribution would have a sharp cutoff at the low end of the specification and more of a tail toward the high end, yet the machining process could be stable under these circumstances.
In the strict sense of a capability study, the shape of a distribution is not as important as how it compares to the engineering specifications. However, if we must express capability as a numeric value, such as the capability indices covered previously, these calculations assume a normal distribution. Remember, all of these indices use the standard deviation calculated using the normal distribution rules. In some cases it may help to understand the characteristics of abnormal distributions and underlying causes. For further reading on this subject refer to the Statistical Quality Control Handbook, by Western Electric Company, or other standard statistical texts.
Tests for Normality
Many distributions are symmetrical and unimodal even if they are not normal (Gaussian). Certain statistical calculations can be completed to help determine if a distribution is truly normal. A brief description of one such calculation follows.
How Calculation Determines the Expected Distribution
One calculation we can complete is chi-square (χ2 ). This calculation determines how well the collected data follows the expected distribution — in this case, the normal distribution. This test is also called a goodness-of-fit test because it determines how well the normal curve fits our data. To complete this calculation, the data is placed into classes (cells). A class is similar to a cell on a histogram. It has an upper and lower boundary and we determine which data points fall between the boundaries of each class. The frequency for each class is determined, and if there are not at least 5 samples in the class, it is combined with the next class. Once this is completed, the chi-square calculation is completed for each class.
The chi-square formula is:
O is the observed frequency and E is the expected frequency, based on the normal distribution. The ∑ means that we add all the class results to obtain the chi-square value. This value is then compared to the value from the chi-square table found in Table A-5 of the Appendix.
The number of degrees of freedom is determined by the number of final classes minus 3. We are estimating 3 statistics (mean, standard deviation, and frequency) to complete this test, which is why we subtract 3 from the number of classes. You begin to see why we need a lot of data to determine if a process is normally distributed and capable.
If we do not have sufficient data, we will not obtain enough classes to complete the goodness-of-fit test. Normally, we select what we call a Confidence Level of 0.95, which corresponds to a significance level or critical-chi square or alpha (Producer’s Risk) value of 0.05. If the computed chi-squared value of the distribution is less than the chi-squared value associated with the critical-chi square (0.05) of the same degree of freedom, the distribution is normal.
For a given degree of freedom, the p value strictly decreases as chi-squared increases. So another way of saying a distribution is normal is if p>(1-confidence level). For example, p value is the percentage point of the chi-squared distribution for a given degree of freedom and chi-squared value. P values are given in Table A-5. Further information concerning chi-square and other tests for goodness-of-fit can be found in most statistical texts.
There are many other methods for determining if a distribution is normal. This has been a brief introduction to the topic. Many of the references at the end of this chapter cover this topic in greater detail.
Other Symmetrical Distributions
Kurtosis
Kurtosis is a measure of the flatness of a curve and can be used to describe curves that are symmetrical but not normal. Kurtosis is symbolized by y2.
- If y2= 0, the curve is normal
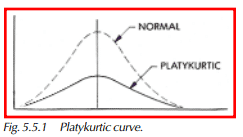
- If y2> 0, the curve is platykurtic
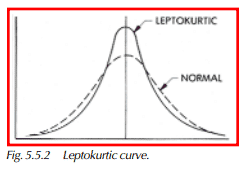
- If y2 < 0, the curve is leptokurtic
Platykurtic Curve
A platykurtic curve has a low, flat peak and a large dispersion with larger, longer tails than a normal distribution (Figure 5.5.1). A leptokurtic curve has a very high peak and shorter tails than a normal distribution (Figure 5.5.2).
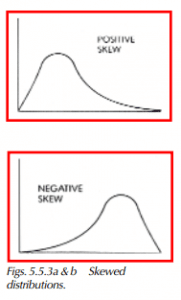
Skewness
(y1) — Skewness is a measure of a distribution’s symmetry. Distributions can be skewed in either a positive or negative direction if one tail extends considerably beyond the other (Figures 5.5.3a and 5.5.3b).
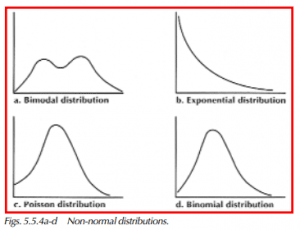
Multi-peaked or Bimodal
These distributions have more than one peak (Figures 5.5.4a-d). A bimodal distribution is characteristic of two mixed distributions, each with a different mean. It is possible that two machines produced the lot, or two operators, vendors, or materials were involved. When separated, each distribution may be normal, but with a different meaning.
Exponential
Exponential curves are often encountered with electronic parts testing (Figure 5.5.4b). The characteristic is having more observations that occur below the mean than above it.