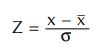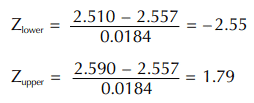What are Histograms
We collect data on our process so we can complete further analysis and decide if any corrective action is needed. The major questions we should ask ourselves are, “How much variation (dispersion) do I have in this variable?” and, “Where is the process centered?” After we collect our data, we can use a histogram to answer these questions. A histogram shows the frequency of occurrence over a specified range of measurements. From the graph, we can get an idea of the shape of our distribution (remember, we are looking for a distribution that is approximately normal), where the process is centered, and the amount of dispersion. Let’s look at how to make a histogram.
How To Make a Histogram
To get a good idea of what our distribution looks like, we need quite a bit of data, about 50-100 data points. Once the data is collected, follow these steps:
1) Find the smallest and largest data points and write them down.
2) Determine the range of the data by subtracting the smallest data point from the largest:
R = X(max) — X(min).
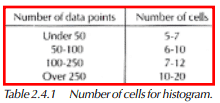
3) Determine the number of cells (bars) that we will have on the histogram using Table 2.4.1. The number of cells is based on the number of data points to be included in the histogram.
4) Divide the range of the data (calculated in step 2) by the number of cells to determine approximately how wide each cell on the histogram should be.
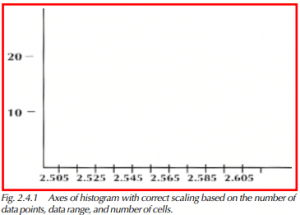
5) Determine the horizontal scale of the histogram as shown in Figure 2.4.1. It must be large enough to extend slightly past the smallest and largest data points.
Specification limits
If we want to include the specification limits on the histogram, we must make sure the scaling is wide enough to include them as well. Also, we should set the boundaries of each cell at a value that will ensure our data cannot fall on a cell boundary. In other words, if our data went out to 0.01, our cell boundaries should go out to 0.015. Or, if all our values are even numbers, the boundaries could be odd number values. This way we will never have a data point fall on the cell boundary, and we will not have to decide in which cell to place the reading.
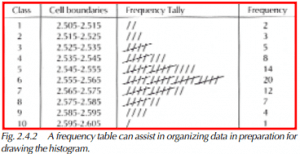
6) Design a frequency table as shown in Figure 2.4.2. Place a tick mark next to the category where each data point falls. Once all data points have been marked in the frequency table, count the number of ticks in each category and write the total in the frequency column. Adding up the numbers in the frequency column should result in the total number of data points collected.
7) Draw a bar on the histogram for each cell. The height of each bar corresponds to the frequency noted on the frequency table.
Once we have drawn all the bars on the histogram, we can calculate the mean of the data and draw a vertical line to note its placement on the histogram. We can also place our specification limits on the histogram as shown in Figure 2.4.3. If the distribution is approximately normal, the standard deviation of the data can be calculated and X ± 3 limits added to the histogram. If the data does not result in a normal curve, refer to the Chapter 5 section on abnormal distributions for more information.
Parts Outside Specifications
If our histogram looks like a normal distribution, we can estimate the percentage of parts outside our specifications. This is done using z-tables or students’ t-tables. Examples of these tables can be found in the Appendix. These tables allow us to estimate the area under some portion of the normal curve — in this case, outside our specifications. In our example, we will use the z-table. Using the z-table assumes we know our sigma — in other words, that we have not estimated standard deviation using a sample of the population. If we do not know sigma, but instead have calculated s(sample standard deviation), we should use the Student’s t-tables. We can calculate the area in the tails of our normal curve that are outside our specification limits using the following formula:
We will complete this formula by first substituting our upper specification then our lower specification for x. These two values are then looked up in a z-table, such as the one provided in the Appendix, Table A-3. Multiplying the number from Table A-3 by 100 gives us the percentage of parts we estimate from the normal curve to be outside first the upper, then lower, specification limits. Let’s run through an example using the data displayed on our histogram. From the histogram, we know our x is 2.557, the lower specification is 2.510, and the upper specification is 2.590. We also know our sigma is 0.0184. Using this data, we can calculate the area under the normal curve that falls outside our specification limits. The calculations are as follows:
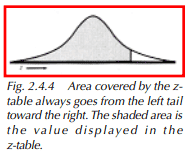
We now refer to Table A-3 (see Appendix) to obtain the area in each tail of the curve. The values obtained from the table are .0054 and .9633 for the lower and upper tails, respectively. Refer to Figure 2.4.4. The z calculation always looks at the area from the left side of the curve toward right (the shaded area of the curve). To get the area above the upper specification limit, we must subtract the z value from 1. In our example, this results in a value of .0367 (1 – .9633) for the area above the upper specification. Multiplying each of the areas gives us a result of 0.54% of parts below the lower specification, and 3.67% above the upper specification.
This is just one example of how z-tables can be used to estimate the area under the normal curve. Additional references at the end of this chapter will cover z-tables and Student’s t-tables in more detail.