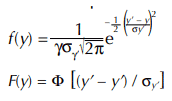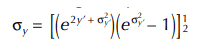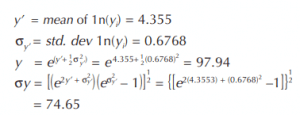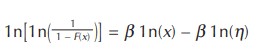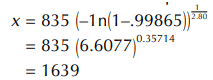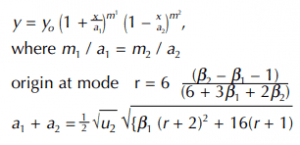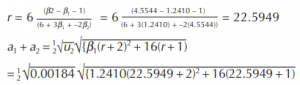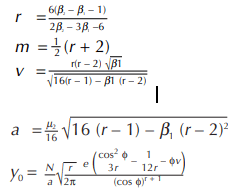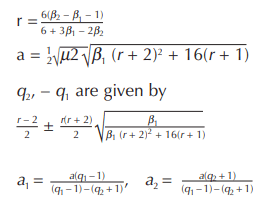What are Non-normal Distributions
Overview
When data are found to not be normally distributed, applying estimation procedures can lead to inaccurate and misleading results. For example, roundness measurements can be less than zero using standard χ – 3σ calculations. The data from roundness measurements are better described using a log-normal or exponential.
Along with these two distributions, there are several other popular curve-fitting techniques: Weibull, Johnson, and Pearson System. Each of these have their own inherent strengths.
Exponential Distribution
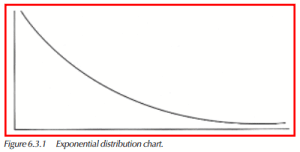
The exponential distribution is a very commonly used distribution in reliability and life testing. It represents the time-to-failure distribution of components, equipment, and systems. The solution to the equation requires that only one parameter be known, the failure rate or, equivalently, the mean time between failures. The shape of the distribution is demonstrated in the figure below. The asymmetrical nature of the distribution puts it on the very edge of the skewness/kurtosis chart, as shown in Figure 6.1.1. The coefficient of skewness is 4.0, and the coefficient of kurtosis is 9.0.
The previous graph demonstrates the exponential pdf, or probability density function. The equation for the pdf is
Where:
= constant failure rate, in failures per unit of measurement. For example, failures per hour, or per million miles,
= 1/m,
m = mean time between failures, or mean time to a failure.
e = 2.718281828,
T = operating time, life, or age.
The cumulative density function, cdf, F(y) is used to determine percentages of the distribution.
For a given percentage, say 99.865%, the point of the distribution, y, is given by
To understand how the pdf and cdf are applied and/or generated, consider the following example.
Example:
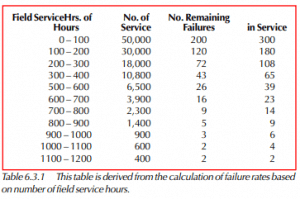
There is a population of circuit boards in the field, say 500. The constant failure rate is 4 failures per 1,000 hrs of use.
The number of failures is estimated by calculating the total number of hours of service, then multiplying by the failure rate. Once items have failed, they are no longer in service. Therefore, the number of available service hours decreases, as does each successive failure count.
For uniform time intervals of 100 hours, the following table may be generated.
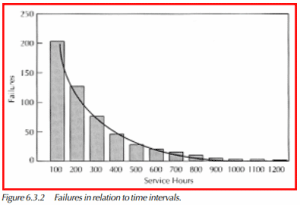
The graph below shows a plot of the failures for each of the time intervals.
From above, the mean time between failures (mtbf) equals the reciprocal of the failure rate (λ). Therefore, with the example of 4 failures per 1,000 hours, or 0.004 failures per hour,
MTBF = (1 / λ ) = 1 / .004) = 250 hrs
The point by which 90% of the units are expected to fail is
y = –m 1n(1 – F(y)) = –250 1n(1 – .90) = 575 hrs.
Log-Normal Distribution
This distribution fits many types of data adequately, because it has a great variety of shapes. This distribution is often useful if the range of the data is several powers of ten. It is often used for economical data, data on response of biological material to stimulus, and certain types of life data, for example, metal fatigue and electrical insulation life.
The pdf and cdf of two-parameter log-normal distribution are given by
Where: y’ = loge y,
y’ = mean of the natural logarithms of the data,
σy’ = standard deviation of the natural logarithms of the data.
The mean of the log-normal distribution is given by,
The standard deviation of the log-normal distribution is given by,
Data are log-normally distributed if the logarithms of the data are normally distributed.
The calculations of mean and standard deviation follow that of the standard normal distribution, except that the calculations use the natural log, or 1n, of the sample data.
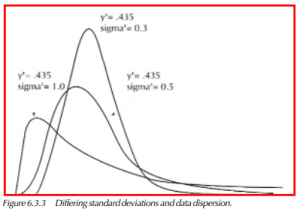
Figure 6.3.3 shows the pdf’s of several distributions having the same mean, but different standard deviations. When viewing the graphic, note that those pdf’s with a greater standard deviation, sigma, have a greater dispersion of data.
Example:
Given the following sample of data, the log-normal mean and standard deviation have been calculated:
30.4, 36.7, 53.3, 58.5, 74.0, 99.3, 114.3, 140.1, 257.9.
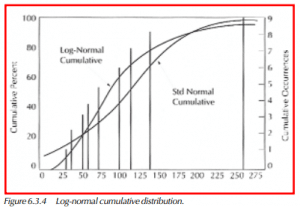
Figure 6.3.4 shows the plot of the log-normal cumulative distribution from the parameters just calculated. In addition, the standard normal cumulative curve has been added to show the difference between the two calculation techniques. The standard normal curve uses a mean of 96.0, and a standard deviation of 70.4.
The 10% point of the distribution is calculated as follows,
where z = –1.282 for the .10 alpha level.
Weibull Distribution
The Weibull distribution is most frequently used within the field of reliability. It provides the best fit of Life Data. This is due in part to the broad range of distribution shapes that are included in the Weibull family. Many other distributions are included either exactly or approximately, including (but not limited to) the Normal and the Exponential. If the fit is poor, other distributions should be considered. The Log-Normal is not a member of the Weibull family.
The Weibull cumulative distribution function, F(x), is as follows,
Where:
F(x) = percentage point of the distribution, ranging from (0<F(x)<1),
e = 2.718281828,
x = point of the distribution,
η = eta, scale parameter,
β = beta, shape parameter
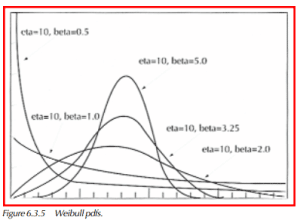
With a shape parameter equal to 1.0, the above cdf equation is identical to that of the exponential distribution. Beta, β, the shape parameter, is what differentiates one Weibull distribution from another. Figure 6.3.5 displays a variety of Weibull pdf’s, all having the same η, or scale parameter. Unlike the scale parameter, the shape parameter, β, is a dimensionless number, i.e., β does not have specific reference to hrs, miles, cycles, etc.
A change of the scale parameter will change the location of the distribution, more so than the shape. Increasing the scale parameter stretches the pdf’s to the right, and decreases the height of the pdf.
The Weibull distribution is quite versatile. Its main drawback is the difficulty in estimating its parameters. Determination of the shape and scale parameters can be done using more than one method. All of the methods are tedious if done manually. The two most popular methods are Linear Regression, and Maximum Likelihood Estimation.
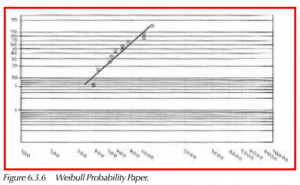
The graphic at right shows Weibull Probability Paper, with some sample data plotted, and a best-fit linear regression line drawn through the points. The shape parameter for this particular example is 2.8, while the scale parameter equals 835.
Sample data set: 390, 418, 526, 560, 581, 725, 738, 794, 1077, 1095, 1242
The scale of the Y-axis is log-log, of the range from .1% to 99.99%. The X-axis is log. In both cases, log implies natural log, or 1n.
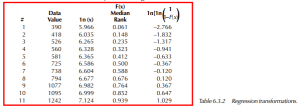
Before a Weibull paper plot can be constructed, there must be some estimates for the Y-axis values. The most commonly used are median ranks. Median ranks are non-parametric estimates of the cumulative distribution based on ordered data. From a sample of 11 values, as above, it is assumed that the first ordered value will lie at or near the cumulative percentage as given by the first median rank. The table below shows a list of sorted data, and the associated median ranks. Plotting the data on the Weibull paper is nothing more than a scattergram, using the Data Values for X’s, and the Median Ranks for Y’s.
Determination of the Weibull Distribution Parameters
The simplest method of calculating the Weibull parameters is to use Linear Regression. The following data table shows the transformations necessary for the regression.
By taking the logarithm of the Weibull cumulative distribution function twice and with some rearranging, the following equation results:
This is the equation of a straight line, (y = mx+b). The slope is β and β 1n(η) is the intercept. Most computer spreadsheets have linear regression routines.
Choose the 1n(x) as the x-range, and 1n[1n( 1 1–F(x))] as the y-range. The output yields a constant, which is the y-intercept, and an x-coefficient, which is the slope. The scale parameter is determined using the following formula,
For the data in the above table, Lotus 1-2-3 reports an x-coefficient of 2.80, which is the shape parameter, β. The constant is reported to be –18.885. Using the above equation,
Using the Weibull Distribution for Process Limit Determination
Once the Weibull distribution parameters have been estimated, it is a straightforward task to calculate various percentages of the distribution. As shown in the beginning of the Weibull section, the cumulative density function (cdf) is
To calculate the point of the distribution at a given percentage, the cdf may be rearranged to the following
where:
F(x) = percentage of distribution, (0<F(x)<1)
x= point of distribution at specified percentage
Using the results from the example above, the 99.865% point of the distribution is
The Three Parameter Weibull Distribution
The Weibull is generally considered to be a two parameter distribution. On occasion, it is practical to add a third parameter. A variety of names can be found for this third parameter, including,
γ, gamma, the location parameter, t0, & minimum life.
How the location parameter is used
The location parameter is used when there is a high degree of certainty that no values will be found less than whatever value is specified as the location parameter.
The net effect of this third parameter is to start the Weibull distribution at a point away from zero. This can improve the fit of the curve to the sample date, thereby improving the accuracy of the reporting.
Determination of the third parameter is best done iteratively. Different values are tried in the regression, and an optimal value is selected based on the correlation coefficient from the regression. The calculations differ in that the location parameter is subtracted from the sample data prior to the regressions. In essence, this shifts the data toward zero, but only for the determination of the Weibull parameters. All results reporting must take into consideration whether a non-zero location parameter is used, e.g., percentage points of the distribution.
Weibull Distribution Summary
The Weibull distribution has the ability to fit a wide variety of skewed distributions. There are, however, limitations to its application, one of which is that the distribution only works with values greater than zero.
It is best to keep in mind that the Weibull distribution can work well for variable data analysis, but its roots are in life data analysis. The types of analysis associated with reliability don’t always lend themselves well as robust curve-fitting solutions
Johnson Transformations
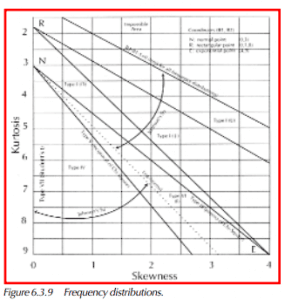
At the beginning of this chapter, there is a diagram showing ranges of skewness and kurtosis. The distributions detailed thus far are shown to have limited scope within the diagram. The Johnson Transformation system, and Pearson System to follow, present methods used to approximate frequency distributions for all those other skewness/kurtosis combinations.
The Johnson Transformation technique proposes a system of curves by a method of translation. The advantage of this system is its close association to the simplicity of the Normal distribution.
Consider a transformation of a variable x to normality,
z = f(x),
where z is a unit normal variable. This defines an infinite system of frequency curves, corresponding to the possible functions f(x) that might be chosen. In other words, by describing f (x) in other terms, with specialized parameters, it is possible to achieve a system of curves that can approximate most frequency distributions. The values of these parameters will determine which curve of the system represents the distribution of x.
Bounded Johnson Curves, Sb
There are two types of curves within the Johnson System, bounded and unbounded. For the bounded curves, one or both of the end-points may be known.
The equation for fitting curves of the bounded type is
Z = γ + δ log { y / (1 – y) } (0 ≤ y ≤ 1),
where Z is an N(0,1) variate. The determination of parameters for the bounded curves is not straightforward, and a table has been formulated to facilitate their calculation. (See Biometrika, Volume XXX, Table 36.)
Values that the table provides are based upon the skewness and kurtosis of the sample data. Four separate values come from the table, γ, δ, µ’ (y), σ(y).
The transformation becomes
Z= γ + δ log {y/(1 – y)} = γ + δ log {(x – ξ)/(ξ + λ – x)}
where λ = σ(x)/σ(y)
and
ξ = µ’(x) – λ µ’(y).
If the skewness (β1) is negative, γ should be replaced by –γ and µ’ by 1 – µ’. The values of δ and σ remain unchanged. Example:
Consider the following table of summarized values,
The mean, µ’ (x), and standard deviation, σ(x), are equal to 0.01100 and 0.00567, respectively. The skewness, as calculated by γ1 = ( µ2 3 µ3 2 ) 1/2 , equals 0.796, and the kurtosis, γ2 = ( µ4 µ2 2 ) – 3, is 3.334.
Using the skewness and kurtosis values, and reading from the aforementioned table in Biometrika results in tabular values of
γ = 1.409,
δ = 1.248,
µ’(y) = 0.270,
σ(y) = 0.145.
From these values we find,
λ = σ(x) / σ(y) = 0.00567 / 0.145 = 0.0392
ξ = µ’(x) – λ µ’ (y) = 0.1100 – 0.0392(0.270)
= 0.00044
ξ + λ = 0.00044 + 0.0392 = 0.03964
Inverting
Z = γ + δ log{(x – ξ)/(ξ + λ – x)} from above, we have
x = [ξ + (ξ + λ) exp{ (Z – γ)/δ}] / [1 + exp{ (Z – γ ) / δ}],
where x is point of the distribution to be estimated, and Z is the standard normal value, e.g., Z = 3.0 = 99.865%.
The inversion allows for the calculation of points of the distribution at specific percentages of the distribution.
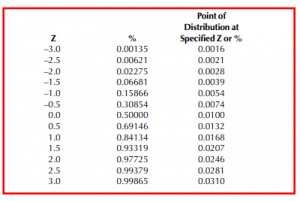
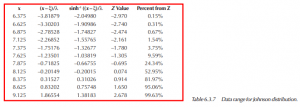
The following table demonstrates the points of the distribution at various Zs with their associated percentages.
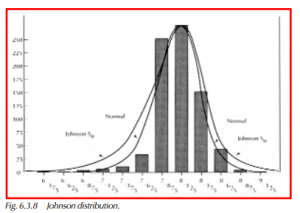
So, for this example, if the Johnson Bounded technique were to be used to calculate process capability at ± 3.0 standard deviations, the table results in 99.865% = 0.0310, 0.00135 = 0.0016.
Process Capability estimate at (99.865%, 0.00135%) = 0.0295. When compared to the standard practice of mean ± 3.0 std dev’s,
0.0110 + 3.0(0.00567) = 0.0280
0.0110 – 3.0(0.00567) = –0.0060
resulting in a process capability estimate of 0.0340.
Using the mean – 3.0 std dev’s to calculate the Lower Process Limit overestimates the deviation of the limit from the mean. This is attributable to the skewness of this particular example.
The Upper Process Limit as calculated by the Johnson Transformation method is greater than that estimated by using the mean +3.0 std dev’s. The largest value from the sample group is 0.030, which is greater than the process limit of 0.028 reported by using the Normal distribution. As the Johnson curve reports the upper limit to be .032, the curve-fitting technique is more accurate. (For this example of 130 values, the upper limit of the population should be expected to be greater than the largest value of the sample.)
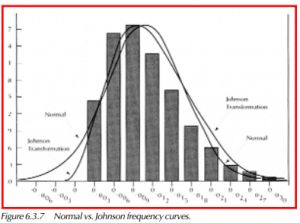
The following graphic displays a histogram with overlays of the Normal and Johnson Sb frequency curves.
Unbounded Johnson Curves, Su
The Johnson Su distributions are unlimited in either direction. They are defined by the relation
Z = γ + δ sinh–1 y (– ∞ < y < ∞)
where Z is an N(0,1) variate, as with the Sb curves above, and y = (x – ξ ) / λ. The determination of parameters for unbounded Johnson transformations is more straightforward than that for the bounded variety. Similar to the SB system, there are values that necessarily come from published tables (see Biometrika,Vol XX).
The mean and variance of y may be expressed as
where w = exp (δ–2) and Ω = γ and δ. γ and δ are tabular values. γ has the opposite sign of β1. In using the Su transformation, if x is the random variable with whose distribution we are concerned, then
y = (x – ξ) / λ,
where λ = σ(x) / σ(y) and ξ = E(x) – λE(y).
To determine where a certain percentage of the distribution falls, e.g., 99.865%, – determine the standard normal value. For 99.865%, the standard normal value is 3.0 – and use the following equation, x = ξ + λ sinh ((Z-γ) / δ
where Z is the standard normal value and
sinh(x) = . 2
Inverting the above to yield a percentage from a point of the distribution,
Z = γ + δ sinh–1 ((x – ξ) / λ)
where x is the point of the distribution for which the percentage is to be determined,
and sinh–1 (x) = 1n (x + √1 + x2 ).
The following example illustrates all of the above equations and demonstrates the ease of the calculations.
Example:
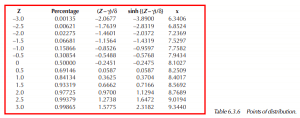
Consider the following table of values:
If the above example were used in a typical process capability study, X ± 3.0σ, the upper limit would lie at 9.3440 and the lower limit at 6.3406. The difference between these two (9.3340 – 6.3406) yields a process capability of 3.0034. In comparing to 6 times the standard deviation, 6 x (0.28332) = 1.6999. Accounting for the data at the lower end of the distribution stretches the fitted curve. The actual range of the data set is 2.750. The following graph displays the Johnson Su distribution for this example.
To calculate percentages of the distribution at a given x, use the previously shown equation, Z = γ + δ sinh–1 ((x – ξ) / λ). The following table demonstrates the calculations and provides results for a variety of points along the data range.
Popular spreadsheet programs such as Lotus 1-2-3 and Excel have the sinh, sinh–1, and cosh functions at your disposal. It is not difficult to use these software packages to perform the calculations described in this section.
Pearson System of Frequency Distributions
This system of frequency distributions was derived by Karl Pearson near the turn of the century. The system involves a variety of different equations, all of different general shapes. Their deviation can be quite complex, and the intent here is to demonstrate the usage, as opposed to explanation.
The Pearson System has shown in practice to be superior to other curve-fitting techniques. The seven different distributions that comprise the system provide the probability density functions only. To use the distributions to estimate cumulative percentages, integral calculus is required, hence the complexity.
The following diagram, repeated from early in the chapter, shows the variety of different Pearson System frequency equations, in regard to where they fall paired with different skewness and kurtosis values.
There is a simple statistic, k, that is used to determine which of the seven types are to be used
The Pearson System of Frequency Distributions
Type 1- Main Type, Beta Function (k<0)
Type 2- Transition, Inverted Student’s t (k=0, β2≠0)
Type 3- Transition, Incomplete Gamma Function (k<<0)
Type 4- Main Type, (0>k>1)
Type 5- Transition, (k=1)
Type 6- Main Type, Inverted Beta Function (k>1)
Type 7- Transition Type
The transition types are the dividing lines of the above graphic. The divisions are between the main types listed above. In general, the main types are more difficult in their derivation. They cover a greater range of skewness/kurtosis area of the graph, and have subsequently more complicated solutions.
The main types shall be discussed as their skewness/kurtosis combinations cover nearly the entire range of distribution shapes.
Type I – Beta Function
The m’s are given by
when µ3 is positive, m2 is the positive root
The usual shape of the curve is like that of the following example, but if m1 and m2 are approximately equal, it is nearly symmetrical. If m1 and m2 are not small, then the curve tails off at both ends. If m1 is negative, the curve is J-shaped. If both m1 and m2 are negative, the curve is U-shaped.
In the case of the J- and U-shaped curves, though the ordinates are infinitive, the area is finite.
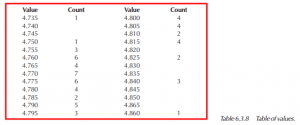
Example:
Consider the table of values
With
Mean = 4.8014 β1 = 1.2410
Std dev = 0.00183 β2 = 4.5544
Starting the calculation with r,
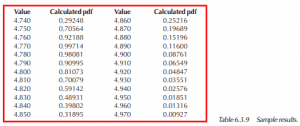
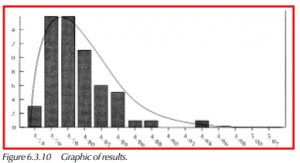
Note that the greatest pdf is found at 4.770, near the mode of 4.7726. To determine process capability, or similarly, the distance between percentiles, integral calculus is required. Simply put, the area beneath the curve must be determined. Then, it becomes a trial/error procedure to find those points at the ends of the curve that represent the 0.135 and 99.865 percentiles, assuming that process capability is defined byX ± 3σ.
For this example, the lower process limit (.135 percentile) lies at xxxxxxx, while the upper process limit (99.865 percentile) is at x.xxxx.
Pearson Type IV
The Pearson Type IV equation for frequency distribution is as follows:
where N is the total count and tanφ = v/r
origin = mean
The curve is skewed and has unlimited range in both directions. µ3 and v have opposite signs (when µ3 is positive, v is negative).
Example:
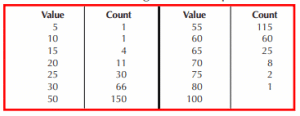
Consider the following table of sample data.
A Chi-Square test rejects the hypothesis of normality (Chi-Square statistic of 71.067, 14 degrees of freedom).
Mean = 44.7949 β1 = .002687
Std Dev = 10.6809 β2 = 3.3636
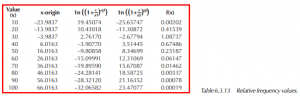
Starting the calculations with r,
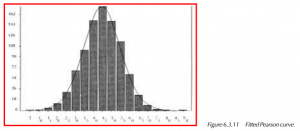
The following graphic displays the fitted Pearson curve to the histogram.
Pearson Type VI
The range is from a to ∞ and the method is like that of Type I. If µ3 is negative, then a is negative, and the range is from –∞ to –a.
r is always negative and q1 is greater than q2. If q2 is negative, the curve is J-shaped. The equation for the curve is
The values, calculated in order are,
Origin is at the Mean.
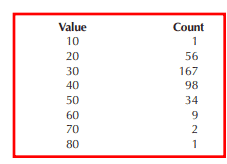
As with Types I and IV a detailed example follows. Consider the following data table.
Providing the statistics,
Mean = 33.9837 β1 = 0.7662
Std Dev = 10.3529 β2 = 4.4453
µ2 = 101.474 µ3 = 894.771
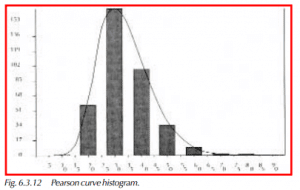
The following graphic displays the fitted Pearson curve to the histogram of the data.
Conclusion
This chapter has touched on the most important information concerning continuous, or non-normal distributions. The bibliography at the end of this chapter provides reference information for those readers who would like more detailed information on the subject.