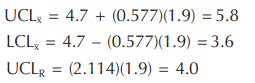What is Shewhart Chart or x̄ & R CHART
This section describes how to make and analyze x & R charts, also known as Shewhart Control Charts. The x & R chart is the most versatile of control charts for variables. There may be specific situations where sigma charts, median charts, and charts of individuals have some advantages over x & R charts; but in most applications, an x & R chart will do as well or better. Since all are similar in methods of usage and analysis, only x & R charts will be treated in depth.
The rationale for x & R Charts
A control chart is used to establish the operating level and variation of a process. Since the parts coming off a process may be infinite in number, we need a way to establish and monitor this operating level and variation without measuring every part. The x & R chart is extremely efficient at this. It also provides a way to avoid the two types of errors that occur when attempting to control a process:
- Type I error — saying a process is unstable when it is stable.
- Type II error — saying a process is stable when it is unstable.
Type I error
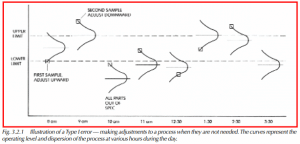
Both of these errors occur when we don’t have a method of identifying assignable causes — when we aren’t thinking statistically about the data. An example of a Type I error is an operator who adjusts the stops on a turret lathe after taking one hourly measurement. The data might look like Figure 3.2.1. He starts out at 8:00 a.m. making a batch of 30 parts. The sideways histogram represents the distribution of those 30 parts measurements, as compared to the nominal and upper and lower limits of the specification. The first batch shows evidence of stable variation (a normal distribution). The mean is very close to the nominal and nearly every piece falls within the limits. Is there a need to adjust the stops? Certainly not. But at 8:00 a.m., he picks up one part and measures it. It happens to be right at the lower limit, so he moves the stops outward. This shifts the operating level of his process. After his next batch, he takes a second sample and finds he is way above the upper limit.
So he moves the stops inward enough to compensate for the shifts. Between 10:00 a.m. and 11:00 a.m., every part he makes is out of specification. In fact, for the whole day, about half of what he produces is out of specification and unusable. Even though the process is stable and capable of making a high proportion of good parts, a large proportion of bad parts are being produced because the operator is taking only one sample and basing his decisions on it. He is making a Type I error. An x & R chart could have told him when to adjust the operating level and by how much. Just as importantly, it could have told him when to leave it alone.
Type II error
A Type II error is also easy to illustrate, as shown in Figure 3.2.2. In this case, the operating level, or mean, is always within specification, but the distribution of data shows evidence of a lack of stability. Imagine an operator taking a measurement that happens to fall within specification and, therefore, not making any adjustments. An x and R chart may possibly have alerted the operator to an out-of-control process after the first hour, and steps could have been taken to correct it.
The difference between the chart shown in Figure 3.2.1 and an x & R chart is that an x & R chart is easier to make. Instead of calculating and graphing small histograms of data subgroups, we graph the averages and ranges on separate charts.
An x & R chart can be made manually or by computer. Some of the graphs shown on the following pages were produced by an IBM PC computer. Since the main calculations are finding the average and range of a set of 5 or so numbers, the charts could also be done manually. The advantages of a computer lie in minimizing errors, improving the readability of the graph, and freeing the auditor to perform the more human tasks of analysis: judgment and action.
Creating an x & R Chart
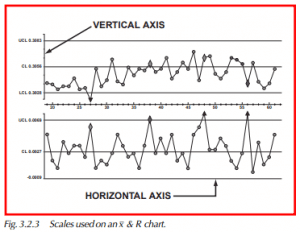
To explain the elements of an x & R chart, it helps to create one from scratch as if we were to do it manually. Figure 3.2.3 is a computer illustration of a chart, but it can also be done manually.
Vertical Scale
The vertical scale of an x chart should have the grand average of the data at the midpoint (Figure 3.2.3). This could also be thought of as the expected operating level of the process. Extending above and below the midpoint should be evenly-spaced scale divisions. The scale increments should be sufficiently wide to graph significant changes in the average. The scale should extend far enough from the midpoint to take in any expected variation. As a rule of thumb, the scale should extend at least 20% beyond any element that would be put on the graph, such as control limits. The R chart should be scaled similarly, with the expected range at the midpoint, and the scale extending at least 40% beyond any element.
Horizontal Scale
The horizontal scale should be the same on both charts. The scale divisions correspond to the frequency of sampling and should be labeled by the hour or date when the data was collected, starting at the left. Data should be collected frequently when starting out, perhaps every hour or even more frequently on a high-volume process. Once the chart is established and the process has evidence of stability, data can be collected less frequently — every other hour or by shift.
Data Collection
An x is the symbol for a single measurement. To start a control chart, at least 100 measurements must be taken for the data to be statistically significant. We can begin plotting averages and ranges right away, but we need at least 100 measurements to add the essential elements of the chart — the grand average and the control limits. Several considerations must be made to ensure that the 100 measurements are representative of the process:
- Measurement devices must be accurate enough to record the differences between samples. The devices must have high repeatability. See Chapter 6 for a discussion of measurement systems.
- Measurements must be made in small groupings at selected intervals. Determining the groupings and intervals is called rational subgrouping and is explained in more detail later. Normally, subgroup size, symbolized by n, can be from 2 to 20 consecutive samples, with n = 5 being the most common.
Plotting the Averages
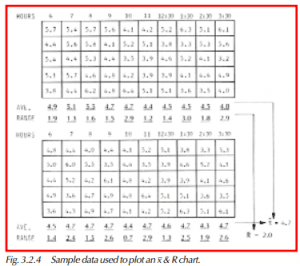
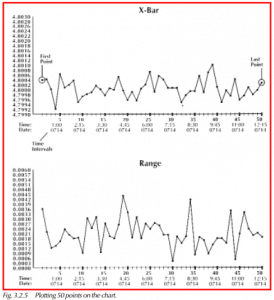
x, pronounced x-bar, is the symbol of the average of a subgroup. The data should be arranged in columns of 5 samples each, whether on a sheet or in a data collector (Figure 3.2.4). Each subgroup is then averaged. The averages are plotted on the chart in the sequence in which they were collected (Figure 3.2.5). Twenty points on the chart will represent 100 measurements in 5 sample subgroups.
Plotting the Ranges
R is the symbol for subgroup range. The range of each subgroup in Figure 3.2.4 is plotted against the intervals when they were collected.
Centerlines
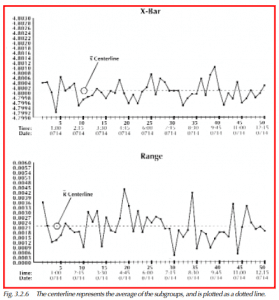
x̄̄, pronounced x-double bar, is the average of the subgroup averages (grand average). See Figure 3.2.4. R-bar is the average of the subgroup ranges. They get plotted as horizontal dotted lines (Figure 3.2.6). They are your first estimate of the operating level of the process.
Control Limits
The control limits on the chart are the estimated ±3 sigma limits for the process. Since sigma must be estimated from samples taken from a continuous process, tables of constants have been developed to make these calculations simple and to reduce error (see Appendix Table A-1 — Factors for Computing Control Chart Lines).
In the formulas above, A2, D4, and D3 are the constants used for calculating control limits, taken from Table A-1. They vary according to subgroup size (n). For n = 5, A2 = 0.577, D3 = 0.0, and D4= 2.114. The chart in Figure 3.2.6 has an xd of 4.7 and an x̄̄ of 1.9, so the control limits for the chart would be:
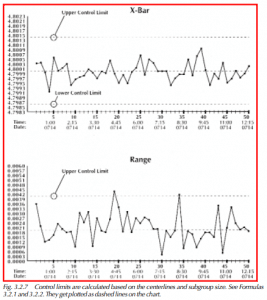
Horizontal dashed lines mark the control limits on the graphs (Figure 3.2.7). By chance alone, the subgroup averages and ranges should fall within these control limits 99.73% of the time. For the most part, the variability that occurs between the control limits can be attributed to common causes. There are certain patterns that occur between the limits that one should learn to recognize, but the most important characteristic to look for is one or more points falling outside the limits. They indicate the influences of assignable causes of variation.
Some Questions about x̄ & R Charts
How many points are needed before control limits can be calculated?
The general rule is at least 20 points, representing 100 measurements. For control limits to be meaningful, they must be based on a representative sample of the population. There must be a high level of confidence that the sample is representative, and that is what 100 measurements or more provide. Fewer than 100 measurements quickly decrease the confidence level. Since we seek to improve quality by detecting assignable causes, we should always aim to make the control limits as statistically significant as possible.
Should engineering limits be put on an x̄ chart?
Engineering limits are an arbitrary demand on a process. The points on the x chart are averages, so a point at or near an engineering limit can mean many things, including the possibility that one or several data measurements are out of limits. In a purely statistical sense, engineering limits, or process objectives, do not belong on x̄ & R charts. However, many industries have to live with these specifications as the criteria for a good process; including them on the chart may serve this goal.
Should the points be connected on the chart?
This is purely a matter of taste. A line connecting the points emphasizes the sequencing of points from left to right. The interpretation of a chart does not depend on this emphasis, so sometimes the sequencing can lead one to the wrong conclusions, like seeing short-term trends that aren’t really there. Lines between points are ornamentation. If they make the chart more appealing to look at and use, then they may be beneficial.
Rational Subgrouping
To make x̄ & R charts truly useful and easy to interpret, they have to be set up that way. This is analogous to a good family portrait. What appears to be a simple photograph of a group of people usually has to be orchestrated by a professional photographer. Quite a bit of expertise and planning must go into portrait photography, and the same is true with rational subgrouping and x̄ & R charts.
Statistical Quality Control Handbook
The main source of information used for this section on rational subgrouping is the Statistical Quality Control Handbook by Western Electric Co., Inc., 1956. A rational subgroup is one where assignable causes create the least variability between measurements within the subgroup itself. If a subgroup has 5 measurements, then the opportunities for variation among those measurements must be made deliberately small. This usually means the subgroup should be taken from a batch of pieces produced under like conditions — one operator and no tooling or material changes. Five consecutive pieces might be the easiest to collect.
Logic behind Rational Subgrouping
The logic behind rational subgrouping is that if we can make variability between pieces within a subgroup entirely due to common causes, then the differences in subgroup averages and ranges will be due to assignable causes. The effects of assignable causes will not be buried within a subgroup and dampened by averaging. They will appear on the chart in the form of points that exceed the control limits or have an identifiable pattern.
Data Collection Planning
When planning the data collection, we must have an understanding of what will constitute a subgroup. If we believe that the time of day a piece is produced contributes to variation between pieces, then one subgroup should be of 5 consecutive pieces from the process. Several subgroups should be collected at selected times throughout the day. If we have a multiple spindle machine and believe that some of the spindles are fine and others not so fine, then the subgroup should be 5 pieces from one spindle and 5 from the next, not one piece off each spindle averaged together.
An x̄ & R chart is used to plot one system of causes. If several different machines contribute to a single lot of parts, an x̄ & R chart of samples taken from the lot will not reveal nearly as much as separate charts on each machine. Using rational subgrouping and working upstream with an x̄ & R chart, we will find that the chart does indeed help identify assignable causes of variation.
x̄ & R Chart Patterns
Characteristics of a Process Showing Stability
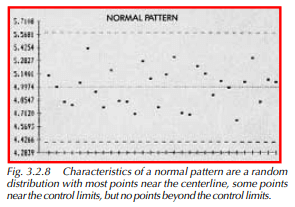
The most common feature of a process showing stability, a constant-cause system, is the absence of any recognizable pattern (Western Electric, 1956). Figure 3.2.8 shows such a process. The points on the chart are randomly distributed between the control limits. Since there is a slight chance of a point falling outside the control limits under normal circumstances, it can happen. A rare point out of limits on a process that has shown stability over the long run can probably be ignored. The characteristics can be summarized as follows:
- Most points are near the centerline.
- Some points are spread out and approach the limits.
- No points are beyond the control limits.
Characteristics of a Lack of Stability
The characteristics of a lack of stability are:
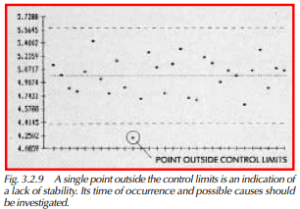
- One or more points are outside the control limits (Figure 3.2.9).
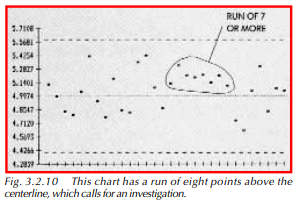
- There is a run of 7or more successive points above or below the centerline (Figure 3.2.10).
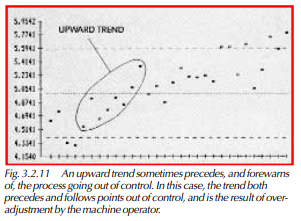
- There is a trend, downward or upward, of 7 or more successive points (Figure 3.2.11).
- There is a cycle, a pattern that repeats itself (Figure 3.2.12).
Note: The number 7 is commonly used for trends and runs, but this is not a hard rule.Since the control limits are at ±3 sigma from the centerline, either side of the centerline can be divided up into three zones at ±1 and ±2 sigma (Western Electric, 1956). These zones (labeled C, B, and A going away from the centerline), although not plotted on the chart, also are used in reading a control chart. See Figure 3.2.13.
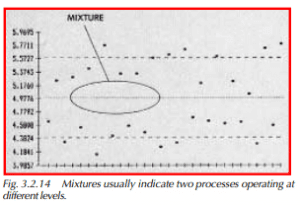
In addition, there are several patterns that may appear which are unnatural and should be investigated (Western Electric, 1956): - a mixture, an absence of points near the centerline (Figure 3.2.14)
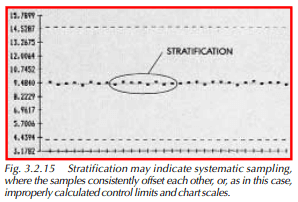
- stratification, 15 or more points consistently hugging the centerline (Figure 3.2.15)
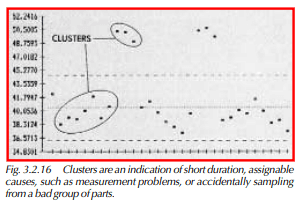
- clusters, the grouping of points in one area of the chart (Figure 3.2.16)
How to Identify Assignable Causes
The first technique to use when looking at an x̄ & R chart is to read the R chart first (Western Electric, 1956). The R chart is more sensitive to changes in uniformity and consistency. If bad parts start appearing in a process, they will affect the R chart. The variation will increase, so some points will be higher than normal. Generally, the lower the points in the R chart, the more uniform the process. Two machines turning out the same parts can be compared for uniformity with their R charts. Parts mixed together from different processes will also show up in the R chart. Intermittent variation, caused by a switch or relay that strikes occasionally, will cause the R chart to go out of control.
Anything that introduces a new system of causes into the process will show up in the R chart. Any change to the process, such as an inexperienced operator, poor materials, tool wear, or a lack of maintenance, will shift points upward. The biggest clues to an assignable cause on an R chart are the time the characteristic occurs, and the fact that some parts are affected more than others. Since the R chart is more sensitive to change, efforts at improving the process will show up first in the R chart. A steady shift downward in points on the R chart is the best evidence of having successfully eliminated assignable causes of variation.
Once the R chart is stable, we can focus on the x̄ chart. When the R chart is unstable, the x̄ chart can be very misleading. When both charts are stable, the process is said to be in control, and the x̄ chart indicates the process operating level at various times. Changes in the operating level can be classed by two types: true x̄ causes and false x̄ causes (Western Electric, 1956).
- True x̄ causes change all pieces from a process at a generally uniform rate. This can include a change in materials (thicker or thinner stock), a temperature change, machine calibration or setup, or gradual tooling wear. These things cause a change in level over time that usually can be traced to the moment they occur.
- False x̄ causes show up because the x̄ chart reflects changes in the R chart, and those causes are better interpreted on the R chart. They include all the causes mentioned above that create dispersion within a subgroup.
Interpreting the x̄ and the R Chart Together
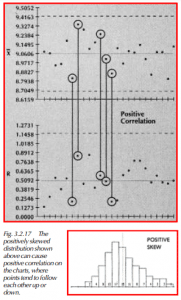
The x̄ chart and the R chart must be interpreted together, as well as separately (Western Electric, 1956). As stated, a stable process will have points randomly distributed between the control limits on the charts. With a stable process, the x̄ & R points should not follow each other. A lack of stability will sometimes cause them to move together. For example, a process whose population is skewed in a positive direction (Figure 3.2.17) with a long tail to the high side, will cause a positive correlation between the x̄ chart and the R chart. In other words, high x̄ points will tend to follow high R points. A process with a negatively skewed population will cause a negative correlation between the charts, as shown in Figure 3.2.18. The x̄ points will tend to follow the R points but in the opposite direction.
Changes in Level
A sustained change in the level of either chart may call for a recalculation of the centerline and control limits. Control limits must reflect the long-term operating characteristics of the process. For that reason, control limits are recalculated only when the sustained change in level appears to be a permanent change. Recalculating limits at that time renews the ability of the control limits to be used to detect assignable causes. It also recognizes a change to the process which, for better or worse, is more or less permanent. A chart can be thought of as a moving window. It should accurately reflect present conditions since that is when action based on the chart must take place. Keeping the centerline and control limits constant causes them to eventually become as arbitrary as engineering limits. We must remember, however, that the control limits should be based on at least 20 points. Any sustained change in level should exist for at least 20 points.
Beyond the x̄ & R Chart
An x̄ & R chart is probably the most effective tool for reducing variability. Throughout this section, the emphasis has been on detecting and working to eliminate assignable causes of variation. One might ask, “But what about the common causes?” Common causes are much more difficult to address on an everyday level. Often, they are part of the whole manufacturing environment, and addressing them often means addressing decisions on materials and equipment purchasing, material handling, shop organization, product and process design, employee education, and company orientation. Obviously, eliminating common causes is beyond the scope of this handbook. The task of assessing a process is a quality function, however. It is known generally as process capability studies and is covered in Chapter 5. Acceptance sampling is another aspect of quality control that deals with common causes and are covered in Chapter 7.