What are the Capability Measures for Non-normal Distributions
In the previous section, we covered methods for determining if a set of data is normally distributed. If we find our data does not at least approximate a normal distribution, the standard capability indices will not give us valid information because they are based on the normal distribution. How, then, do we measure process capability if the data is not normally distributed? That is the subject of this section. This section assumes the reader has a more indepth understanding of statistical techniques than do previous sections. Much of the analysis of non-normal distributions is beyond the scope of this handbook.
The First Tool of Non-normal Process
The first tool for determining the capability of a non-normal process is visual inspection of a histogram. Specification limits may be placed on the histogram and the data examined for parts outside specification limits. If all parts are well within the specification limits, we have shown graphically that our process is capable. Remember, if the data is non-normal we cannot use either the estimated formula or the standard formula for standard deviation because they are both based on the normal distribution.
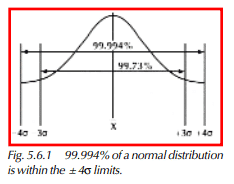
Let’s look back for a moment at what we were trying to accomplish when we expressed capability with indices such as CP and CpK. With those indices, we aimed for values of 1.33 or greater. This correlated to ±4σ capability, or 99.994% of all parts within the specifications (see Figure 5.6.1). If this was our target with normal distributions, why not carry it over to our analysis of non-normal distributions? If we can show that 99.994% or more of our parts are within specification, the process is capable.
How the Data Can Be Transformed
One statistical method of showing capability requires first transforming the data to approximate a normal distribution. The data can be transformed by taking its natural logarithm (ln). After calculating the average and standard deviation of the transformed data, we can use z-tables (Chapter 2). The natural log of the specifications must also be calculated. Using the z values calculated for the area outside of the specification limits, we can also calculate the percentage of parts inside the specification limits. In this way, we can express the process capability numerically.
How the Capability of Process Can Be Expressed
If we are working with a distribution where there is a natural barrier at 0 (Figure 5.6.2), we are only concerned with the area above the upper specification limit. The capability of the process can then be expressed as the percentage of parts between 0 and the upper specification limit.
Another option in this case is to calculate the CpK for just the upper half of the distribution. Because we know no parts can be below 0, only the upper half of the curve is of concern. We cannot calculate CP, however, because there is no lower tail to this type of distribution.
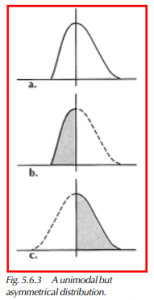
If we are working with a distribution that is not symmetrical but is unimodal, we may consider looking at the curve as two halves (Figure 5.6.3). The mode should be used as the determination of central tendency. Each half is drawn separately and its mirror image added to give two normal distributions. Each curve can then be analyzed for the percentage outside the appropriate specification limit.
In Figure 5.6.3, we would calculate the area below the lower specification limit using curve b, and calculate the area above the upper specification limit using curve c. The average and standard deviation of each curve (b and c) must be calculated, as well as the z values for the area outside the specification. Once the area outside the specification limit is calculated for each curve, the area within the specification is found by subtracting the area outside the appropriate specification from 0.50 (remember, we are only looking at the shaded half of b and c). The percentage within the specification limits for the original curve is obtained by adding the two results for a percentage within the specification for b and c. This, then, gives us a numerical result for process capability.
These are just a couple of methods for dealing with non-normal distributions. Many other methods are available, such as Weibull distributions, but they involve a higher level of statistical knowledge. Further information can be obtained from standard statistical texts and computer software packages. The method chosen should be appropriate for the process distribution in question and must be understandable to the end-user.