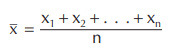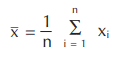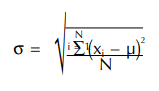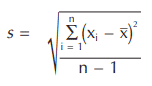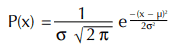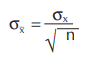What are the Basic Statistical Concepts
What Shewhart discovered in the ’20s is that variability is as normal to a manufacturing process as it is to natural phenomena like the movement of molecules in a jar of fluid. No two things can ever be made exactly alike, just as no two things are alike in nature. The key to success in manufacturing is to understand the causes of variability and to have a method that recognizes them. Shewhart found two basic causes of variability: common causes and assignable causes.
Common Causes of Variability
Probability and Chance
If we flip a coin and count the number of heads versus tails, at first we may get a few more of one than the other but over the long run, they will be fairly even (Figure 1.3.1). We say that the probability of heads in a coin toss is 50% or 0.5. Probability is a statistic. For a few coin flips, this probability may not be a reliable indicator of the outcome, but it tends to be more reliable as larger groups of coin tosses are counted. Coin tosses may vary purely by chance, and chance is what is known as a common cause of variability.
Unequal Frequency Distribution
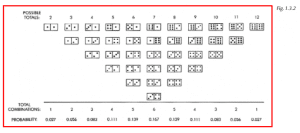
Another example of common causes at work is the throw of the dice. If we repeatedly throw a pair of dice and record the totals, we will get an unequal distribution of results. The possible outcomes are the numbers 2 through 12, but as any craps game player will tell us, the frequency of their occurrence varies. Dice pair combinations total some numbers more frequently than others, as shown in Figure 1.3.2. The number 7 will occur in six combinations whereas the number 12 has only one. Over the long run, the probability of the number 7 occurring is .167 or about 17%, which is greater than the number 2, which is about 3%. A pair of dice produces an example of an unequal frequency distribution, but it is entirely due to common causes.
Constant-Cause System
Whenever the outcomes of a process can be expressed in probabilities, and we are certain about the distribution of outcomes over the long run, we have what is known as a constant-cause system.
As you may have guessed, manufacturing processes sometimes behave like constant-cause systems. The causes of variation are commonplace like dice throws. If left to produce parts continually without change, the variation would remain. It cannot be altered without changing the process itself. Statistics provide us with ways of recognizing variation due to common causes. The main one is the control chart. By using a control chart we can separate common causes from the second type, which are called assignable causes.
Assignable Causes of Variability
A change of materials, excessive tooling wear, a new operator — these types of things would produce variation in a process that is different from variation due to common causes. They disturb a process so that what it produces seems unnatural. A loaded pair of dice is another example. Since we know what a regular pair of dice produces over a large number of rolls, we can be reasonably sure a pair of dice is loaded if, after a large number of rolls, we have more 12s than 7s.
When we look for problems in a process we are usually just looking for these assignable causes of variability. Assignable causes produce erratic behavior for which a reason can be identified. One might ask why we are going through all the trouble. Why separate assignable causes from common causes when we have to compare parts to a specification anyway? One reason is that we can minimize variability when we know its causes. The less variability we have in our parts, and the closer they are to the target, the happier our customers will be. They will be confident in our ability to supply a good, consistent product with few or no parts out of specification. On the other hand, large variability may result in parts being out of specification.
Choices for many parts of the specification
If there are many parts out of specification, we have three choices: 1) continually inspecting all parts and using the good ones, 2) improving the process until most or all parts are good, or 3) scrapping the process and building a better one. Since 100% inspection is expensive and inefficient in most cases, we are better off trying to improve the process and reducing our inspection load — which brings us back to the process. There is no sense in trying to improve a process that won’t do the job for us. Also, we don’t want to scrap a process that potentially could work like a charm. Therefore, we need a way to determine whether the process can consistently produce good parts. The only reliable method is through the use of control charts to find and eliminate the assignable causes of variation.
Basic Statistical Terms
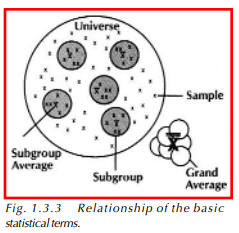
Before we go on to the basic statistical concepts presented in the following sections, there are some terms that we need to discuss. Refer to Figure 1.3.3 as these terms are presented.
Sample Term
As we collect data, we pull samples from the process. A sample is an individual piece of measurement that we collect for analysis. Samples are usually pulled in rational groups called subgroups. Groups of samples that are pulled in a manner that shows little variation between parts within the group, such as consecutive parts off a manufacturing line, are considered rational subgroups.
Mean Term
Once we have collected the samples that make up our subgroup, we can calculate the average of this data, otherwise called the mean. The symbol used to represent the mean is x, pronounced x-bar. We can continue to collect our subgroups at regular intervals. Once we have collected a number of subgroups and calculated the mean of each one, we can also calculate the overall average of the data. This is called the grand average and is represented by X. As we have been collecting data, we have pulled just a few samples from all of the parts we manufacture. All of the parts we make constitute a population or universe. It would be very difficult and time-consuming to measure every part manufactured, so we use the samples and statistical analysis to give us an idea of what all of the parts in our universe look like. The statistical concepts that are used to make conclusions about the universe are introduced in the following sections of this chapter and the remaining chapters.
Measures of Central Tendency
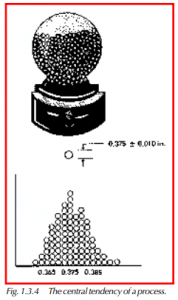
Many processes are set up to aim at a target dimension. The parts that come off the process vary, of course; but we always hope they are close to the nominal and that very few fall outside of the high and low specifications. Parts made in this way exhibit what is called a central tendency. That is, they tend to group around a certain dimension (Figure 1.3.4).
The most useful measure of central tendency is the mean or average. To find the mean of measurement data, add the data together and divide by the number of measurements taken. The formula would be:
Each x is a measurement and n is the number of measurements. In statistics, the average is symbolized by x. If we use the Greek letter for summation ∑, the formula can be written as:
There are two additional measures of central tendency that can be used. The first is the median, which is the middle of our data. The median splits our data in half, so 50% of our parts are above the median, and 50% are below. The second measure of central tendency is the mode, which is the most frequently occurring value in our data.
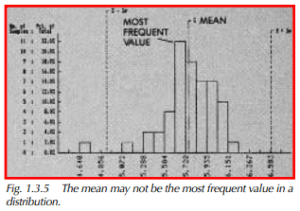
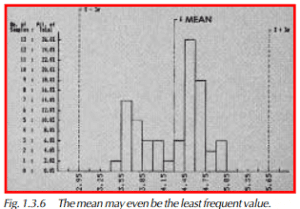
Figure 1.3.5 is a histogram showing one dimension and its variation among 50 parts. The histogram shows the frequency of parts at each dimension by the height of the bars. Notice that the x is not at the most frequent value. The most frequent value (mode) is just to the left of it. Now, look at Figure 1.3.6. The mean value in this histogram seems to be among the least frequent values that occurred. Obviously, without some kind of statistic that tells us about the spread or dispersion of our data, the mean does not tell us enough. Averages are used in many sports, from bowling to baseball. When we know someone’s bowling average or baseball hitting average we have some indication of how good that person is, but not really enough information about consistency. Lurking behind a low average could be a lot of great games and a few very bad ones. A good average could merely be the work of an average player with a few lucky games.
Range and Standard Deviation (Sigma)
Two measures of dispersion are used in statistics, the range and the standard deviation.
Range Formula
The range tells us what the overall spread of the data is. To get the range, subtract the lowest from the highest measurement. The symbol for range is R. The formula is:
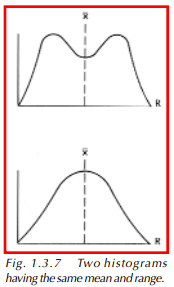
This formula simply tells us to subtract the smallest measurement from the largest. Now that we have a measure of spread and a measure of central tendency, why do we need a third statistic? What does standard deviation tell us that range and average do not? To help answer this, we need to look at Figure 1.3.7. Two different histograms are pictured. Rather than bars, continuous lines are used to show the shape of the distributions. We can imagine that if enough data was collected, and if the data was represented by bars of very narrow width, a bar histogram would look nearly like the curves shown here.
Standard Deviation Formula
The two histograms have different shapes, yet the ranges and averages are the same. This is when we use the standard deviation. Standard deviation uses all of the data displayed on the histogram, not just the highest and lowest points, and gives us a better idea of what the distribution looks like.
The standard deviation of a population (universe) is called sigma in statistics and is symbolized by the Greek letter σ. Sigma can be calculated using this formula:
µ is the mean of the data, x is an individual measurement, and N is the total number of measurements in the universe. It is not very often that we calculate the sigma because measuring all of the parts in the universe is very time-consuming. Instead, we estimate the population standard deviation by pulling samples and calculating the sample standard deviation s. The formula for s is:
This formula is called the n-1 formula because of its denominator. The more classic standard deviation formula uses n instead of n-1. The n-1 formula will be used here because it provides a closer approximation of the standard deviation of samples coming from a process that is producing continually. Continuous processes are the most common type used in manufacturing. Sigma has a special relationship to the distribution shown in Figure 1.3.8. It is called the normal distribution, and its properties are described in the next paragraph.
The Normal Distribution
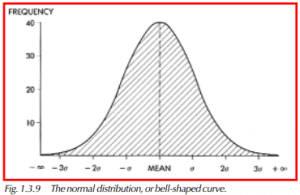
There is one type of distribution that can be described entirely by its mean and standard deviation. It is the normal (Gaussian) distribution or bell-shaped curve. It has these characteristics (Figure 1.3.9):
- The mean equals the mode, which equals the median.
- It is symmetrical about the mean.
- It slopes downward on both sides to infinity. In other words, it theoretically has an infinite range.
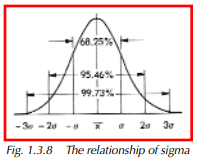
- 68.25% of all measurements lie between x – σ and x + σ. See Figure 1.3.8.
- 95.46% of all measurements lie between x – 2σ and x + 2σ.
- 99.73% of all measurements lie between x – 3σ and x +3σ.
The equation for a bell-shaped curve is:
The normal distribution is a valuable tool because we can compare the histogram of a process to it and draw some conclusions about the capability of the process. Before making this type of comparison, however, a process must be monitored for evidence of stability over time. This is done by taking small groups of samples at selected intervals, measuring them, and plotting their averages and ranges on a control chart. The control chart provides us with an indication of whether we have stable variation — in other words, a constant-cause system — or a lack of stability due to some assignable causes. Chapter 2 describes the making and using of x & R charts in more detail. The reason they work has to do with the central limit theorem and the normal distribution curve.
Central Limit Theorem
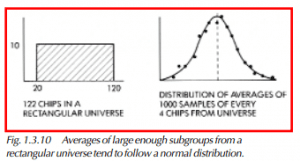
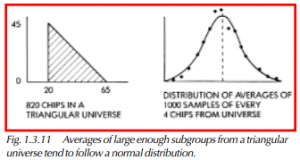
Shewhart found that the normal distribution curve appears when the averages of subgroups from a constant-cause system are plotted in the form of a histogram. The constant-cause system does not itself have to be a normal distribution. It can be triangular, rectangular, or even an inverted-pyramid shape like dice combinations, as long as the sample size is reasonably large. The averages of different-sized subgroups selected from these distributions, or universes, as they are called in statistics, will show a central tendency. The variation of averages will tend to follow the normal curve. This is called the central limit theorem.
How Stewhart Demonstrated Central Limit Theorem
Shewhart demonstrated this by using numbered chips and a large bowl. His normal bowl had 998 chips, his rectangular bowl had 122, and his triangular bowl had 820. The rectangular universe had chips bounded by a certain range and in equal numbers, like in Figure 1.3.10. The triangular universe had unequal numbers of various chips, as shown in Figure 1.3.11. Shewhart took each chip out of the bowl one at a time, recorded the number, and put it back. He then mixed the bowl before choosing another. He averaged every four. The points he plotted fell within or along the edges of the bell-shaped curve. What this meant to him is that a process can be monitored over time by measuring and averaging a standard subgroup of parts. The subgroup could be 2, 4, or even 20. The frequency could be once per hour, or once per day, depending upon the output. If the process was a constant-cause system, these averages would fall within a normal curve. One could conclude that the process was stable. By stable, we mean that the variability was entirely due to common causes. Statisticians also use the phrase in control to refer to a process that has stable variability over time.
Frequently checking the averages of subgroups also provides a way to discover when assignable causes are present in a process. When assignable causes appear, they will affect the averages to the point where these averages will probably not fit within a normal curve. Once the stable variation of the process is known, the assignable causes will appear in averages of subgroups taken periodically.
How To Calculate the Standard Deviation
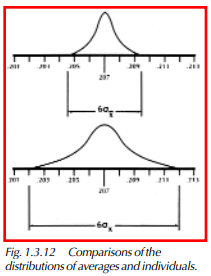
We can calculate the standard deviation of the averages and, if compared to the standard deviation of the individual samples, we will find it is smaller, as shown in Figure 1.3.12. σx is the symbol we use to represent the standard deviation of the averages. It is related to the standard deviation of the individuals by the formula:
σx is the standard deviation of the individuals, and n is the number of samples in the subgroup. Control charts work because, in the real world, measurements of the same feature on a number of parts tend to cluster about a fixed value in a manner described by the central limit theorem. The charting of averages has this particular advantage over the charting of individual data points. The charting of ranges is also used because subgroup ranges will also show stability if a constant-cause system exists.
The SPC concepts presented here will be explained further throughout Part I. Chapters 2 through 5 will deal specifically with some of these concepts and how they are implemented with SPC.