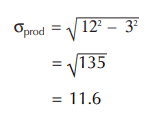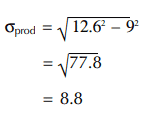How to Reduce Measurement Error
Tolerances and Measurement Error
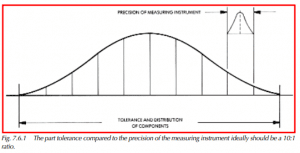
It is recommended that the ratio of the product tolerance to the precision of the measuring instrument be a 10:1 ratio for an ideal condition. In a worst-case condition, a 5:1 ratio can be used. These are rules of thumb; the actual ratio should be based on the level of confidence required for each situation. When the tolerance is mixed with the measurement error, a good component may be diagnosed as being bad, or a bad component may be accepted. See Figure 7.6.1 for an example of a 10:1 precision versus part tolerance distribution.
Analysis of Measurement Error (Capability)
Section 7.5 described many sources of measurement error. The error causes variations in the observed values (measurements). Conclusions can be drawn about measurement error based on the formula below. The relationship of various causes is assumed to be independent.
The causes are not always easy to identify and may be interrelated. Often it is feasible to identify causes by experiment. Generally, measurement variation occurs because of variation in the system of measurement and variation in the product being measured. This can be expressed as follows:
If the variation in the system of measurement is less than 10% of the observed variation, then the effect upon the variation in product will be less than 1%. The rule of thumb of 10% variation is based on the statement below.
The following examples will illustrate this concept. To determine the amount of variation within a product group, samples were selected and measured using the same measuring device. The observed variation, or standard deviation, was found to be 12. Next, a number of repeat measurements were taken on the same sample, using the same measuring device, and the observed variation, or standard deviation was found to be 3. Product variation was then calculated to be:
It can be seen that the measurement variation has a small impact on the product variation by comparing the observed variation and the calculated product variation. There is about a 3% difference between the observed variation and the product variation.
In another example, the observed variation was 12.6 and the variation of measurement was 9. The product variation was calculated at 8.8.
Where product variation and measurement variation are almost the same, further evaluation is needed to determine if the measurement variation can be reduced to a more acceptable level.
Minimizing Instrument Error
Accuracy and precision can be controlled if appropriate steps are taken. If a systematic error is evident, then a correction can be applied to the data. If the accuracy is low, then a correction factor can be added to each measurement to adjust the data to the proper reading. An adjustment could also be made to the instrument to bring it back into calibration.
What are Calibration Programs
Calibration programs are a means of checking equipment used for quality inspection. Calibration control would include provisions for periodic audits on instruments to check their accuracy, precision, and general condition. New equipment should be included in a calibration program to ensure it is properly functioning before use in an inspection process.
Inventory control of instruments
Inventory control of instruments is often used and recorded to keep track of the use and calibration of instruments. Calibration schedules are kept on instruments as a means to monitor instrument conditions. Elapsed calendar time is the most widely-used method. Checks are made at calendar intervals to monitor the instrument’s performance. Another method is to schedule calibration by the actual usage. This is done by counting the number of measurements an instrument has made. Metering the hours of use is also a technique for monitoring calibration intervals.
Adherence to calibration schedules is probably the most important aspect of calibration control. Without this, the calibration schedule’s value would be greatly reduced. Many systems can be used to accomplish this adherence.
Tool Control Charts
To minimize the effects of calibration intervals on the observed variation of a process, it is recommended that control charts be kept on all auditing tools. The charts can be placed on the gauging fixture or taken on the audit route. An extra reading, the tool control reading, should be included with each subgroup. For example, if five samples are taken on each item in an audit route, then the sixth should be the tool control reading, and it should be plotted on a chart.
Using tool control charts is the only reliable method of corroborating data from the current process with historical data. The tool control chart can be used to compensate for any bias due to measurement error when trying to equate the data. The charts will also provide a time-independent indication of a need for calibration or repair.
Reducing Operator Errors
Adequate training is required for the operators of instruments to be able to properly utilize them. Many errors can be introduced into measurement by variation in operator technique. With the use of training, these types of errors can be reduced. Proper test procedures and fixturing will also help reduce errors in measurement. Procedures will give a documented systematic approach to the way a test or inspection is to be performed. These procedures should include enough detail to prevent differences in tests or inspections from one operator to the next. Test procedures themselves should be checked to ensure that they are fully useful and properly designed. It does no good for operators to follow a procedure that does not provide the desired results.
Automation of measurement can be an effective means to reduce operator errors in the recording of data. An instrument that automatically records its measurements will eliminate transposition errors and other types of recording errors. Not only do automated instruments reduce errors, but in many cases, the time required to record measurements is markedly reduced.